
| A. | [$\frac{1}{7}$,$\frac{1}{5}$]∪{3} | B. | [3,5)∪{$\frac{1}{7}$} | C. | [$\frac{1}{7}$,$\frac{1}{3}$]∪{5} | D. | [3,7)∪{$\frac{1}{5}$} |
分析 若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0且a≠1)的图象上关于直线x=1对称的点有且仅有一对,则函数y=logax,与y=|x-5|-1上有且只有一个交点,解得:实数a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0且a≠1)的图象上关于直线x=1对称的点有且仅有一对,
∴函数y=logax,与y=|x-5|-1上有且只有一个交点,
当对数函数的图象过(5,-1)点时,a=$\frac{1}{5}$,
当对数函数的图象过(3,1)点时,a=3,
当对数函数的图象过(7,1)点时,a=7,
故a[3,7)∪{$\frac{1}{5}$},
故选:D
点评 本题考查的知识点是分段函数的应用,函数的图象,数形结合思想,难度中档.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
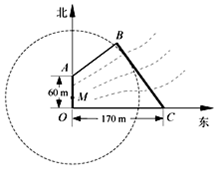 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=$\frac{4}{3}$.
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com