练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图．
    （I）求直方图中的a值；
    （II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数．说明理由．

    分析 （1）由频率分布直方图能求出a的值．
    （2）由频率分布直方图先求出月均用水量不低于3吨的频率，由此能求出全市居民中月均用水量不低于3吨的人数．

    解答 解：（1）由频率分布直方图可知：
    2a×0.5=1-（0.08+0.16+0.42+0.50+0.12+0.08+0.04）×0.5，
    解得a=0.30．
    （2）由频率分布直方图得月均用水量不低于3吨的频率为：
    （0.12+0.08+0.04）×0.5=0.12，
    由样本估计总体得全市居民中月均用水量不低于3吨的频率为0.12，
    所以全市居民中月均用水量不低于3吨的人数约为0.12×30=3.6（万）．

    点评 本题考查实数值的求法，考查频数的求法，是基础题，解题时要认真审题，注意频率分布直方图的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=$\frac{{{x^2}+1}}{bx+c}$的定义域为{x∈R|x≠0}，且f（1）=2．
    （1）求f（x）的解析式；
    （2）判断函数f（x）在[1，+∞）上的单调性，并用定义证明结论；
    （3）求函数在区间[1，2]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．由三条曲线y=$\sqrt{x}$，x轴及直线y=x-2所围成的图形的面积是$\frac{16}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．设a＞b＞0，m=$\sqrt{a}$-$\sqrt{b}$，n=$\sqrt{a-b}$，则m，n的大小关系是m＜n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知直线l1：y=x+1与直线 l2关于点（1，1）对称，则l2的方程是（　　）
    A．2x+y-12=0B．2x+y+3=0C．x-y+3=0D．x-y-1=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．如图，在△ABC中，AB⊥BC，∠BDA=90°，E是BC的中点．求证：∠ABD=∠EDC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{|x-5|-1，3≤x≤7}\end{array}\right.$（a＞0且a≠1）的图象上关于直线x=1对称的点有且仅有一对，则实数a的取值范围是（　　）
    A．[$\frac{1}{7}$，$\frac{1}{5}$]∪{3}B．[3，5）∪{$\frac{1}{7}$}C．[$\frac{1}{7}$，$\frac{1}{3}$]∪{5}D．[3，7）∪{$\frac{1}{5}$}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

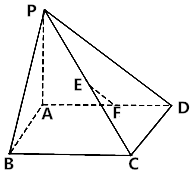    14．如图，四棱锥P-ABCD的底面ABCD是正方形，PA⊥平面ABCD，PA=AB=2．
    （1）若E，F分别是PC，AD的中点，证明：EF∥平面PAB；
    （2）若E是PC的中点，F是AD上的动点，问AF为何值时，EF⊥平面PBC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=log4（4x+1）+kx与g（x）=log4（a•2x-$\frac{4}{3}$a），其中f（x）是偶函数．
    （Ⅰ） 求实数k的值；
    （Ⅱ） 求函数g（x）的定义域；
    （Ⅲ） 若函数f（x）与g（x）的图象有且只有一个公共点，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案