
分析 (I)令f(-x)=f(-x)恒成立,根据对数的运算性质解出k;
(II)令a•2x-$\frac{4}{3}$a>0,对a进行讨论得出x的范围;
(III)令f(x)=g(x),使用对数的运算性质化简,令2x=t,则关于t的方程只有一正数解,对a进行讨论得出a的范围.
解答 解:(I)f(x)的定义域为R,
∵f(x)=log4(4x+1)+kx是偶函数,
∴f(-x)=f(x)恒成立,
即log4(4-x+1)-kx=log4(4x+1)+kx恒成立,
∴log4$\frac{{4}^{-x}+1}{{4}^{x}+1}$=2kx,即log4$\frac{1}{{4}^{x}}$=2kx,
∴42kx=4-x,∴2k=-1,即k=-$\frac{1}{2}$.
(II)由g(x)有意义得a•2x-$\frac{4}{3}a$>0,即a(2x-$\frac{4}{3}$)>0,
当a>0时,2x-$\frac{4}{3}$>0,即2x>$\frac{4}{3}$,∴x>log2$\frac{4}{3}$,
当a<0时,2x-$\frac{4}{3}$<0,即2x<$\frac{4}{3}$,∴x<log2$\frac{4}{3}$.
综上,当a>0时,g(x)的定义域为(log2$\frac{4}{3}$,+∞),
当a<0时,g(x)的定义域为(-∞,log2$\frac{4}{3}$).
(III)令f(x)=g(x)得log4(4x+1)-$\frac{1}{2}$x=log4(a•2x-$\frac{4}{3}a$),
∴log4$\frac{{4}^{x}+1}{{2}^{x}}$=log4(a•2x-$\frac{4}{3}a$),即2x+$\frac{1}{{2}^{x}}$=a•2x-$\frac{4}{3}a$,
令2x=t,则(1-a)t2+$\frac{4}{3}$at+1=0,
∵f(x)与g(x)的图象只有一个交点,
∴f(x)=g(x)只有一解,∴关于t的方程(1-a)t2+$\frac{4}{3}$at+1=0只有一正数解,
(1)若a=1,则$\frac{4}{3}t$+1=0,t=-$\frac{3}{4}$,不符合题意;
(2)若a≠1,且$\frac{16}{9}{a}^{2}$-4(1-a)=0,即a=$\frac{3}{4}$或a=-3.
当a=$\frac{3}{4}$时,方程(1-a)t2+$\frac{4}{3}$at+1=0的解为t=-2,不符合题意;
当a=-3时,方程(1-a)t2+$\frac{4}{3}$at+1=0的解为t=$\frac{1}{2}$,符合题意;
(3)若方程(1-a)t2+$\frac{4}{3}$at+1=0有一正根,一负根,则$\frac{1}{1-a}$<0,∴a>1,
综上,a的取值范围是{a|a>1或a=-3}.
点评 本题主要考查了偶函数的性质,以及对数函数图象与性质的综合应用,同时考查了分类讨论的思想,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 051 | B. | 052 | C. | 053 | D. | 055 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
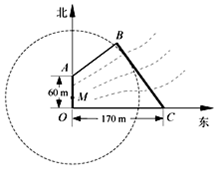 如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=$\frac{4}{3}$.
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=$\frac{4}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3\sqrt{10}}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com