考点:平面向量的综合题
专题:平面向量及应用
分析:(1)由已知得得(2-2sinA)•(1+sinA)-(cosA+sinA)•(sinA-cosA)=2-2sin
2A-sin
2A+cos
2A=3-4sin
2A=0,由此能求出角A的大小和求角B的取值范围.
(2)y=2sin
2B+cos
=
sin2B-cos2B+1=sin(2B-)+1,
B∈(,),由此能求出其单调性并求其值域.
解答:
解:(1)
=(2-2sinA,cosA+sinA)与
=(sinA-cosA,1+sinA)共线,
得(2-2sinA)•(1+sinA)-(cosA+sinA)•(sinA-cosA)
=2-2sin
2A-sin
2A+cos
2A=3-4sin
2A=0,
由A为锐角得
sinA=,从而A=
,
又因为锐角三角形,
B∈(0,),且C=π-A-B∈(0,)解得
B∈(,).
(2)
y=2sin2B+cos()=2sin2B+cos()=
1-cos2B+cos(-2B)=1-cos2B+cos2B+sin2B=
sin2B-cos2B+1=sin(2B-)+1,
B∈(,),
该函数在
(,)上单调递增,在
(,)上单调递减,
2B-∈(,),
y=sin(2B-)+1∈(,2].
点评:本题考查角A的大小和求角B的取值范围的求法,考查函数y=2sin
2B+cos
的单调性的讨论并求其值域,是中档题.



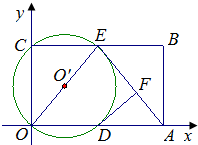 如图,在平面直角坐标系中,矩形ABCO的面积为24,边OA比OC大5.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为24,边OA比OC大5.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.