
 .
.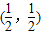 成中心对称;
成中心对称;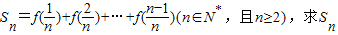 ;
;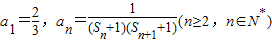 ,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.
,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.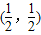 成中心对称也可证明.
成中心对称也可证明.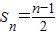 ,因此求得an,利用裂项相消法可以求得{an}的前n项和为Tn,于是由Tn<λ(Sn+1+1)得到 λ与n的关系式进一步利用函数与方程的思想转化为求函数的最值问题,可解得λ 的取值范围.
,因此求得an,利用裂项相消法可以求得{an}的前n项和为Tn,于是由Tn<λ(Sn+1+1)得到 λ与n的关系式进一步利用函数与方程的思想转化为求函数的最值问题,可解得λ 的取值范围.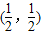 的对称点为N(x1,y1),
的对称点为N(x1,y1),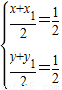 ,∴
,∴ ①.
①.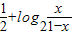 ,即
,即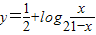 ②.
②.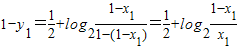 =
=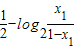 ,
, ,∴N(x1,y1)也在f(x)图象上,∴f(x)图象关于点
,∴N(x1,y1)也在f(x)图象上,∴f(x)图象关于点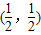 成中心对称.
成中心对称.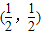 成中心对称,也可给分)(5分)
成中心对称,也可给分)(5分)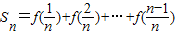 ③,
③,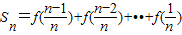 ④
④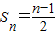 .(9分)
.(9分)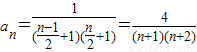 =
=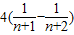 ,
,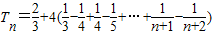 =
=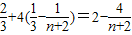 ;
;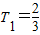 也适合上式,∴
也适合上式,∴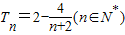 .
.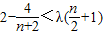 ,∴
,∴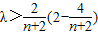 ,即
,即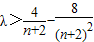 .
.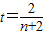 ,则
,则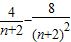 =
=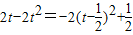 ,
,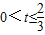 ,
,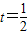 时,即n=2时,
时,即n=2时,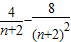 最大,它的最大值是
最大,它的最大值是 ,∴
,∴ .(14分)
.(14分)

科目:高中数学 来源:2012-2013学年宁夏高三第五次月考理科数学试卷(解析版) 题型:解答题
(本小题满分l0分)选修4—5:不等式选讲
已知函数 .
.
(1)求证: ;
;
(2)解不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三上学期10月月考数学卷 题型:解答题
(本题满分15分)已知函数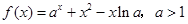 .
.
(I)求证: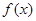 在
在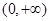 上单调递增;
上单调递增;
(Ⅱ)函数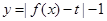 有三个零点,求
有三个零点,求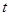 值;
值;
(Ⅲ)对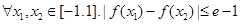 恒成立,求
恒成立,求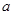 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com