


 •
•
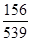 ;(Ⅱ)没有90%的把握认为“大学生上网时间与性别有关”.
;(Ⅱ)没有90%的把握认为“大学生上网时间与性别有关”.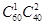 种,则易得概率恰有1人上网时间少于60分钟的
种,则易得概率恰有1人上网时间少于60分钟的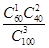 ;(Ⅱ)根据男生、女生的上网时间频数分布表易得2×2列联表,并由
;(Ⅱ)根据男生、女生的上网时间频数分布表易得2×2列联表,并由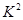 公式得出
公式得出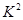 值,即得结论.
值,即得结论.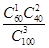 4分
4分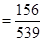 6分
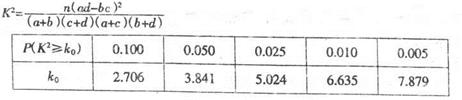
6分| | 上网时间少于60分 | 上网时间不少于60分 | 合计 |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合计 | 130 | 70 | 200 |
 , 10分
, 10分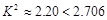 ,∴没有90%的把握认为“大学生上网时间与性别有关”. 12分
,∴没有90%的把握认为“大学生上网时间与性别有关”. 12分

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源:不详 题型:解答题
| 高校 | 相关人数 | 抽取人数 |
| A | 18 | 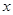 |
| B | 36 | 2 |
| C | 54 | 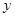 |
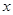 ,
,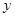 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
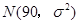 ,其中
,其中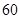 分以下的考生人数占
分以下的考生人数占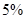 ,则数学成绩在
,则数学成绩在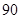 至
至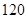 分之间的考生人数所占百分比约为 ( )
分之间的考生人数所占百分比约为 ( )A.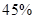 | B.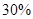 | C.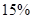 | D.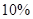 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 时间 | 第一天 | 第二天 | 第三天 | 第四天 |
| 温差(℃) | 9 | 10 | 8 | 11 |
| 发芽数(粒) | 33 | 39 | 26 | 46 |
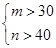 ”的事件A的概率.
”的事件A的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.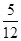 | B.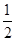 | C.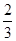 | D.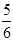 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
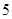 个红球,
个红球,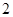 个白球和
个白球和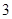 个黑球,乙罐中有
个黑球,乙罐中有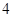 个红球,
个红球,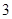 个白球和
个白球和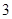 个黑球。先从甲罐中随机取出一球放入乙罐,分别以
个黑球。先从甲罐中随机取出一球放入乙罐,分别以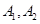 和
和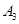 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以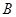 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。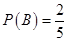 ; ② 事件
; ② 事件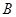 与事件
与事件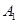 相互独立; ③
相互独立; ③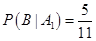
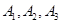 是两两互斥的事件;
是两两互斥的事件; 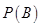 的值不能确定,因为它与
的值不能确定,因为它与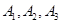 中哪一个发生有关
中哪一个发生有关查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
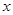 、
、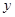 ,设
,设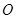 为坐标原点,点
为坐标原点,点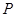 的坐标为
的坐标为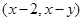 ,记
,记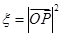 .
.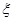 =5的概率;
=5的概率;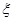 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com