
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起,
使得△ABD与△ABC成直二面角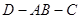 ,如图二,在二面角
,如图二,在二面角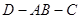 中.
中.
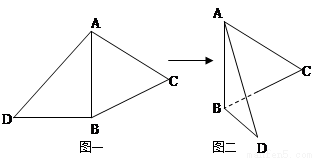
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
(1)根据线面垂直的性质定理来得到线线垂直的证明。关键的一步是利用面ABD 面ABC,得到
面ABC,得到 BD
BD 面ABC,加以证明。
面ABC,加以证明。
(2) 2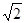 (3)
(3)
【解析】
试题分析: 解:(1)依题意,面ABD 面ABC,AB是交线,
面ABC,AB是交线,
而BD AB,
AB, BD
BD 面ABC,又AC
面ABC,又AC 面ABC,
面ABC,
 BD⊥AC;
4分
BD⊥AC;
4分
(2)由(1)知,BD面ABC,而BC 面ABC,
面ABC,
 BD⊥BC;Rt
BD⊥BC;Rt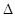 DBC中,BC=BA=2,BD=2,
DBC中,BC=BA=2,BD=2,
 DC=
DC=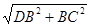 =
= =2
=2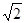 ;
8分
;
8分
(3)取AB的中点H,连CH、DH和DC,

 △ABC是正三角形,
△ABC是正三角形,
 CH
CH AB,又
AB,又 面ABC
面ABC 面ABD,
面ABD,
 CH
CH 面ABD,
面ABD,
 DH是DC在面ABD内的射影,
DH是DC在面ABD内的射影,

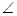 CDH是DC与面ABD成的角。
CDH是DC与面ABD成的角。
而CH=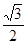 BC=
BC=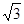 ,由(2)DC=2
,由(2)DC=2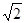 ,
,
 sin
sin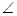 CDH=
CDH=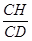 =
= =
= 即为所求。
12分
即为所求。
12分
考点:空间中点线面的位置关系
点评:解决该试题的关键是熟练的运用判定定理和性质定理得到垂直的证明,以及角的求解,属于基础题。


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
 选考题
选考题| 1 | ||
|
|
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.| BF |
| FC |
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.
(2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
D、H、G为垂足.若将正△ABC绕AD旋转一周所得的圆锥体积为V,则其中由阴影部分所产生的旋转体的体积与V的比值为多少?

图6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com