[题目]如图所示.已知几何体的三视图.用斜二测画法画出它的直观图．题目和参考答案——青夏教育精英家教网—

【题目】如图所示，已知几何体的三视图，用斜二测画法画出它的直观图．

【答案】解：①作出长方体的直观图ABCD－A1B1C1D1 ，如图a所示；
②以上底面A1B1C1D1的对角线交点为原点建立x′，y′，z′轴，如图b所示，在z′上取点V′，使得V′O′的长度为棱锥的高，连接V′A1 ， V′B1 ， V′C1 ， V′D1 ，得到四棱锥的直观图，如图b；
③擦去辅助线和坐标轴，遮住部分用虚线表示，得到几何体的直观图，如图c．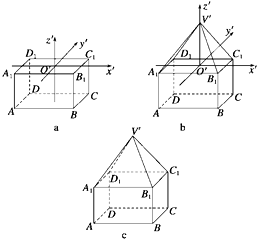

【解析】由三视图还原出几何体是一个长方体与四棱锥的组合体.由斜二测画法规则,画出几何体的直观图.
【考点精析】掌握空间几何体的直观图是解答本题的根本，需要知道立体图形的直观图要严格按照斜二测画法，在直观图中，原来与轴平行的线段仍然与轴平行，角的大小一般都会改变．

练习册系列答案

扬帆文化100分培优智能优选卷系列答案

多维互动提优课堂系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在正方体ABCD－A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ与平面PAO平行？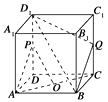

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在一个不透明的箱子里装有5个完全相同的小球，球上分别标有数字1、2、3、4、5．甲先从箱子中摸出一个小球，记下球上所标数字后，将该小球放回箱子中摇匀后，乙再从该箱子中摸出一个小球．
（1）若甲、乙两人谁摸出的球上标的数字大谁就获胜（数字相同为平局），求甲获胜的概率；
（2）规定：两人摸到的球上所标数字之和小于6，则甲获胜，否则乙获胜，这样规定公平吗？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校在校学生2 000人，为了学生的“德、智、体”全面发展，学校举行了跑步和登山比赛活动，每人都参加而且只参与其中一项比赛，各年级参与比赛的人数情况如下表：

	高一年级	高二年级	高三年级
跑步人数	a	b	c
登山人数	x	y	z

其中a∶b∶c＝2∶5∶3，全校参与登山的人数占总人数的 .为了了解学生对本次活动的满意程度，从中抽取一个200人的样本进行调查，则高三年级参与跑步的学生中应抽取( )
A.15人
B.30人
C.40人
D.45人

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知指数函数y=f（x）、对数函数y=g（x）和幂函数y=h（x）的图象都经过点P（），如果f（x1）=g（x2）=h（x3）=4，那么x1+x2+x3=（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在棱长都相等的四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是 ( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面ABC
D.平面PAE⊥平面ABC

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知c＞0，且c≠1，设p：函数y=cx在R上单调递减；q：函数f（x）=x2﹣2cx+1在（，+∞）上为增函数，若“p且q”为假，“p或q”为真，求实数c的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C： + =1（a＞b＞0）的离心率为，其左、右焦点为F1、F2 ，点P是坐标平面内一点，且|OP|= ， = ，其中O为坐标原点．

（1）求椭圆C的方程；
（2）如图，过点S（0，﹣ ）的动直线l交椭圆于A、B两点，是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出点M的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=e2x+1﹣2mx﹣ m，其中m∈R，e为自然对数底数．
（1）讨论函数f（x）的单调性；
（2）若不等式f（x）≥n对任意x∈R都成立，求mn的最大值．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学