
 是一个观光区的平面示意图,建立平面直角坐标系,使顶点
是一个观光区的平面示意图,建立平面直角坐标系,使顶点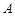 在坐标原点
在坐标原点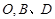 分别为
分别为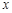 轴、
轴、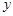 轴,
轴,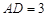 (百米),
(百米),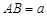 (百米)(
(百米)(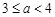 )观光区中间叶形阴影部分
)观光区中间叶形阴影部分 是一个人工湖,它的左下方边缘曲线是函数
是一个人工湖,它的左下方边缘曲线是函数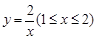 的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段
的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段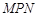 相切(切点记为
相切(切点记为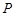 ),并把该观光区分为两部分,且直线
),并把该观光区分为两部分,且直线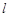 左下部分建设为花圃.记点
左下部分建设为花圃.记点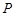 到
到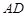 的距离为
的距离为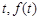 表示花圃的面积.
表示花圃的面积.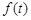 的表达式;
的表达式;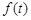 的最小值.
的最小值.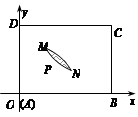
 ;(2)
;(2)
 左下部分花圃的形状,故先求过点
左下部分花圃的形状,故先求过点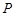 的求切线方程,根据横截距和纵截距的取值范围分为三类:①
的求切线方程,根据横截距和纵截距的取值范围分为三类:①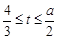 ;②
;②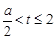 ;③
;③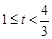 ,花圃形状分别为直角三角形、直角梯形、直角梯形,因其面积表达式不同,故分类三类,并以分段函数的形式给出;(2)分段函数是一个函数,故可分段来求最小值,再比较,哪个值最小,哪个即最小值.当
,花圃形状分别为直角三角形、直角梯形、直角梯形,因其面积表达式不同,故分类三类,并以分段函数的形式给出;(2)分段函数是一个函数,故可分段来求最小值,再比较,哪个值最小,哪个即最小值.当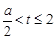 时,
时,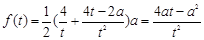 ,;利用导数来求最小值;当
,;利用导数来求最小值;当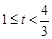 时,
时,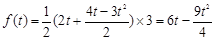 ,利用二次函数的图象来求最小值.
,利用二次函数的图象来求最小值.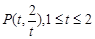 ,又因
,又因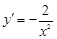 ,所以过点
,所以过点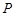 的切线方程为
的切线方程为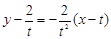 ,即
,即 ,
,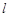 与
与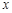 轴交于点
轴交于点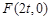 ,与
,与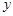 轴交于点
轴交于点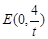 ,
,
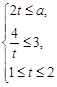 ,即
,即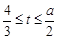 时,切线左下方区域为直角三角形.
时,切线左下方区域为直角三角形.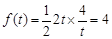 ;
;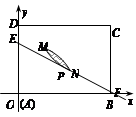
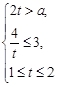 ,即
,即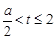 时,切线左下方区域为直角梯形.
时,切线左下方区域为直角梯形.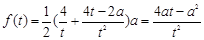 ;
;
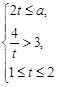 ,即
,即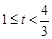 时,切线左下方区域为直角梯形.
时,切线左下方区域为直角梯形.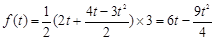 ;
; 7分
7分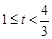 时,
时,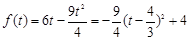 ,当
,当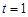 时,
时,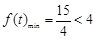 ;
;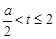 时,
时,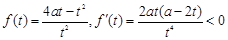 ,
,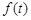 在
在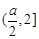 上递减,所以
上递减,所以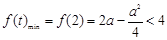 ,
,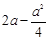 与
与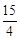 的大小,由于
的大小,由于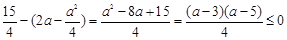 ,
,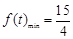 即求. 13分
即求. 13分

科目:高中数学 来源:不详 题型:解答题
 .
. 的单调性;
的单调性; 的图象在点(2,f(2))处的切线的倾斜角为
的图象在点(2,f(2))处的切线的倾斜角为 ,对于任意的
,对于任意的 ,函数
,函数 在区间(t,3)上总不是单调函数,求m的取值范围;
在区间(t,3)上总不是单调函数,求m的取值范围;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com