
【题目】为了解甲、乙两奶粉厂的产品质量,采用分层抽样的方法从甲、乙两奶粉厂生产的产品中分别抽取16件和5件,测量产品中微量元素![]() 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 170 | 178 | 166 | 176 | 180 |
| 74 | 80 | 77 | 76 | 81 |
(1)已知甲厂生产的产品共有96件,求乙厂生产的产品数量;
(2)当产品中的微量元素![]() 满足
满足![]() 且
且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
【答案】(1)30;(2)18;(3)分布列见解析,期望为![]() .
.
【解析】分析:(1)设乙厂生产的产品数量为![]() 件,由
件,由![]() ,即可求得乙厂生产的产品数量;
,即可求得乙厂生产的产品数量;
(2)由题意,从乙厂抽取的![]() 件产品中,编号为
件产品中,编号为![]() 的产品是优等品,即
的产品是优等品,即![]() 件产品中有
件产品中有![]() 件是优等品,由此可估算出乙厂生产的优等品的数量;
件是优等品,由此可估算出乙厂生产的优等品的数量;
(3)![]() 可能的取值为
可能的取值为![]() ,求得取每个随机变量时的概率,得到分布列,利用公式求解数学期望.
,求得取每个随机变量时的概率,得到分布列,利用公式求解数学期望.
详解:(1)设乙厂生产的产品数量为![]() 件,则
件,则![]() ,解得
,解得![]()
所以乙厂生产的产品数量为30件……………………3分
(2)从乙厂抽取的5件产品中,编号为2、5的产品是优等品,即5件产品中有3件是优等品
由此可以估算出乙厂生产的优等品的数量为![]() (件)………………6分
(件)………………6分
(3)![]() 可能的取值为0,1,2
可能的取值为0,1,2
![]()
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
……………………10分
∴![]() ……………………12分
……………………12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ![]() ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为 ![]() ,猜对第3条的概率为
,猜对第3条的概率为 ![]() .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司开设的某险种的基本保费为![]() 万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
本年度出险次数 |
|
|
|
|
|
|
下一次保费(单位:万元) |
|
|
|
|
|
|
设今年初次参保该险种的某人准备来年继续参保该险种,且该参保人一年内出险次数的概率分布列如下:
一年内出险次数 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
(![]() )求此续保人来年的保费高于基本保费的概率.
)求此续保人来年的保费高于基本保费的概率.
(![]() )若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出
)若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
(![]() )求该续保人来年的平均保费与基本保费的比值.
)求该续保人来年的平均保费与基本保费的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年春季,世界各地相继出现流感疫情,这已经成为全球性的公共卫生问题.为了考察某种流感疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 | 未感染 | 总计 | |
注射 | 10 | 40 | 50 |
未注射 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
参照附表,在犯错误的概率最多不超过__________的前提下,可认为“注射疫苗”与“感染流感”有关系.
(参考公式:![]() .)
.)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣4:极坐标与参数方程
极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ![]() ,曲线C2的极坐标方程为ρsinθ=a(a>0),射线
,曲线C2的极坐标方程为ρsinθ=a(a>0),射线 ![]() ,
, ![]() 与曲线C1分别交异于极点O的四点A,B,C,D.
与曲线C1分别交异于极点O的四点A,B,C,D.
(Ⅰ)若曲线C1关于曲线C2对称,求a的值,并把曲线C1和C2化成直角坐标方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知海岛![]() 在海岛
在海岛![]() 北偏东
北偏东![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物体甲从海岛
海里,物体甲从海岛![]() 以
以![]() 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛![]() 移动,同时物体乙从海岛
移动,同时物体乙从海岛![]() 沿着海岛
沿着海岛![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小时的速度移动.
海里/小时的速度移动.
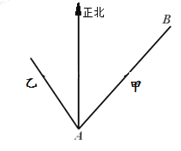
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛![]() 到达海岛
到达海岛![]() 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求圆![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设平面直角坐标系![]() 中的点
中的点![]() ,经过点
,经过点![]() 倾斜角为
倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com