
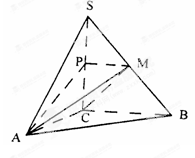

 面
面 由
由 是
是 的中点,易得
的中点,易得 ,所以证明方向转为
,所以证明方向转为 平面
平面 ,又
,又 ,所以只需找出
,所以只需找出 ,而这由
,而这由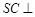 平面
平面 可得,(2)求二面角,关键问题在作出二面角的平面角 作二面角的平面角方法主要是找出二面角棱的垂面,而这在题中易得,即
可得,(2)求二面角,关键问题在作出二面角的平面角 作二面角的平面角方法主要是找出二面角棱的垂面,而这在题中易得,即 平面
平面 异面直线所成角关键找平移,所以过点
异面直线所成角关键找平移,所以过点 作
作 于
于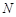 点,使直线
点,使直线 平移到直线
平移到直线 在把空间角转化为平面角后,只需找三角形解出即可
在把空间角转化为平面角后,只需找三角形解出即可 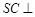 平面
平面 ,
, ,又因为
,又因为
 ,
, ,
, 平面
平面 ,
, 是
是 的中点
的中点 ,
, 面
面 ,所以面
,所以面 面
面 5分
5分 平面
平面 ,
, ,从而
,从而 为二面角
为二面角 的平面角,
的平面角, 与直线
与直线 所成的角为
所成的角为
 作
作 于
于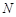 点,连结
点,连结
 在
在 中,由勾股定理得
中,由勾股定理得
 中,
中,
 中,
中,


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:不详 题型:解答题
 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段 上,且
上,且 ,
,
 取何值,总有
取何值,总有 .
. 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
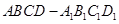 中,
中,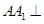 平面
平面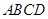 .
.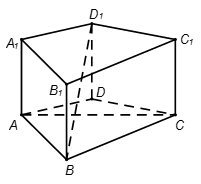
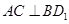 的充分条件,并给予证明;
的充分条件,并给予证明;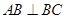 ,②
,②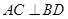 ;③
;③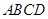 是平行四边形.
是平行四边形.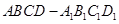 的所有棱长都为1,且
的所有棱长都为1,且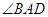 为锐角,求平面
为锐角,求平面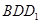 与平面
与平面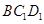 所成锐二面角
所成锐二面角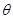 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
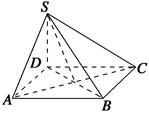
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
| D.AB与SC所成的角等于DC与SA所成的角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com