Question

【题目】已知函数 是定义在 上的奇函数，且 偶函数 的定义域为 ，且当 时， .若存在实数 ，使得 成立，则实数 的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】∵ 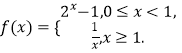，∴当0≤x≤1时，2x﹣1∈[0，1]，
当x≥1时， ∈（0，1]，即x≥0时，f（x）的值域为[0，1]，
∵f（x）是定义在R上的奇函数，∴x≤0时f（x）的值域为[﹣1，0]，∴在R上的函数f（x）的值域为[﹣1，1]．
∵定义在{x|x≠0}上的偶函数g（x），x＞0的g（x）=log2x，∴g（x）=log2|x|（x≠0）
∵存在实数a，使得f（a）=g（b）成立，∴令﹣1≤g（b）≤1．即﹣1≤log2|b|≤1．即有 ≤|b|≤2，∴ ≤b≤2或﹣2≤b≤﹣ ．所以答案是：D．
【考点精析】认真审题，首先需要了解函数奇偶性的性质(在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇)，还要掌握对数的运算性质(①加法：②减法：③数乘：④⑤)的相关知识才是答题的关键．