练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现有2名男生和3名女生． （Ⅰ）若其中2名男生必须相邻排在一起，则这5人站成一排，共有多少种不同的排法？
    （Ⅱ）若男生甲既不能站排头，也不能站排尾，这5人站成一排，共有多少种不同的排法？

    【答案】解：（Ⅰ）若2名男生相邻排在一起，可看成一个元素，与另外3个女生任意排，有 种排法，2名男生任意排，有2种方法，

    根据分步乘法计数原理，共有2×4!=48种不同的排法

    （Ⅱ）若男生甲既不能站排头，也不能站排尾，则甲有3种排法，另外4人任意排，有 种排法，

    根据分步乘法计数原理，共有3×4!=72种不同的排法


    【解析】（Ⅰ）若2名男生相邻可捆绑看成一个元素，与另外3个女生任意排，有 种排法，对捆绑的2名男生松绑，有2种方法，根据分步乘法计数原理，可得答案；（Ⅱ）先排甲有3种排法，另外4人任意排，有 种排法，利用分步乘法计数原理可得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的右焦点为F（1，0），且点 在椭圆C上，O为坐标原点． （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）设过定点T（0，2）的直线l与椭圆C交于不同的两点A、B，且∠AOB为锐角，求直线l的斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知PA⊥平面ABCD，且四边形ABCD为矩形，M、N分别是AB、PC的中点．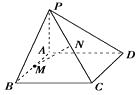

    （1）求证：MN⊥CD；
    （2）若∠PDA＝45°，求证：MN⊥平面PCD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直角梯形ABCD如图所示，分别以AB、BC、CD、DA所在直线为轴旋转，试说明所得几何体的大致形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 是奇函数且当 时是减函数，若 ，则函数 的零点共有（ ）
    A.4个
    B.5个
    C.6个
    D.7个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，a为正常数．
    （1）若f（x）=lnx+φ（x），且 ，求函数f（x）的单调增区间；
    （2）若g（x）=|lnx|+φ（x），且对任意x1 ， x2∈（0，2]，x1≠x2 ， 都有 ，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f：A→B是A到B的一个映射，其中 ，f：(x，y)→(x－y，x＋y)，求与A中的元素(－1,2)相对应的B中的元素和与B中的元素(－1,2)相对应的A中的元素．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 与 是定义在同一区间 上的两个函数，若函数 （ 为函数 的导函数），在 上有且只有两个不同的零点，则称 是 在 上的“关联函数”，若 ，是 在 上的“关联函数”，则实数 的取值范围是（ ）．
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝(m2－m－1)x－5m－3，m为何值时，f(x)：

    (1)是幂函数；

    (2)是正比例函数；

    (3)是反比例函数；

    (4)是二次函数．

    查看答案和解析>>

    同步练习册答案