
【题目】已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):
(1)是幂函数;
(2)是正比例函数;
(3)是反比例函数;
(4)是二次函数.
【答案】(1)m=2或m=-1.(2)m=-![]() .(3)m=-
.(3)m=-![]() .(4) m=-1.
.(4) m=-1.
【解析】试题分析:(1)根据幂函数的定义可知m2-m-1=1,解方程即可;
(2)根据正比例函数的定义知-5m-3=1,再检验系数即可;
(3))根据反比例函数的定义知-5m-3=-1,再检验系数即可;
(4)若f(x)是二次函数,则-5m-3=2,再检验系数即可.
试题解析:
(1)∵f(x)是幂函数,
故m2-m-1=1,即m2-m-2=0,
解得m=2或m=-1.
(2)若f(x)是正比例函数,
则-5m-3=1,解得m=-![]() .
.
此时m2-m-1≠0,故m=-![]() .
.
(3)若f(x)是反比例函数,
则-5m-3=-1,
则m=-![]() ,此时m2-m-1≠0,
,此时m2-m-1≠0,
故m=-![]() .
.
(4)若f(x)是二次函数,则-5m-3=2,
即m=-1,此时m2-m-1≠0,故m=-1.


科目:高中数学 来源: 题型:
【题目】现有2名男生和3名女生. (Ⅰ)若其中2名男生必须相邻排在一起,则这5人站成一排,共有多少种不同的排法?
(Ⅱ)若男生甲既不能站排头,也不能站排尾,这5人站成一排,共有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1的离心率为
=1的离心率为 ![]() ,点F1 , F2是椭圆E的左、右焦点,过F1的直线与椭圆E交于A,B两点,且△F2AB的周长为8.
,点F1 , F2是椭圆E的左、右焦点,过F1的直线与椭圆E交于A,B两点,且△F2AB的周长为8.
(1)求椭圆E的标准方程;
(2)动点M在椭圆E上,动点N在直线l:y=2 ![]() 上,若OM⊥ON,探究原点O到直线MN的距离是否为定值,并说明理由.
上,若OM⊥ON,探究原点O到直线MN的距离是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断函数 ![]() 的单调性并给出证明;
的单调性并给出证明;
(2)若存在实数 ![]() 使函数
使函数 ![]() 是奇函数,求
是奇函数,求 ![]() ;
;
(3)对于(2)中的 ![]() ,若
,若 ![]() ,当
,当 ![]() 时恒成立,求
时恒成立,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
(1)求椭圆C的方程,并写出其参数方程;
(2)求动点P到直线l:x+2y﹣9=0的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有A、B两个景点,位于一条小路(直道)的同侧,分别距小路![]() km和2
km和2![]() km,且A、B景点间相距2 km,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳观赏和拍摄效果,则观景点应设于____.
km,且A、B景点间相距2 km,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳观赏和拍摄效果,则观景点应设于____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( ) 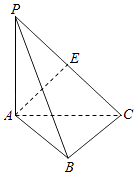
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=sinx+ ![]() cosx的图象向右平移φ(φ>0)个单位长度得到函数y=sinx﹣
cosx的图象向右平移φ(φ>0)个单位长度得到函数y=sinx﹣ ![]() cosx的图象,则φ的最小值为( )
cosx的图象,则φ的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com