
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
(1)求椭圆C的方程,并写出其参数方程;
(2)求动点P到直线l:x+2y﹣9=0的距离的最小值.
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】设集合A={x|-1≤x≤6},B={x|m-1≤x≤2m+1},已知BA.
(1)求实数m的取值范围;
(2)当x∈N时,求集合A的子集的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,平面 ![]() 平面
平面 ![]() ,四边形
,四边形 ![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.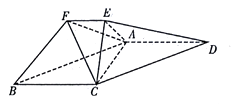
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)求 ![]() 到平面
到平面 ![]() 的距离;
的距离;
(3)求三棱锥 ![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C1的方程为(x﹣2)2+y2=4.以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2,射线C3的极坐标方程为 ![]() .
.
(1)将曲线C1的直角坐标方程化为极坐标方程;
(2)若射线C3与曲线C1、C2分别交于点A、B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):
(1)是幂函数;
(2)是正比例函数;
(3)是反比例函数;
(4)是二次函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m、高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A′B′C′D′中:
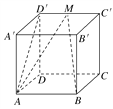
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ∥
∥![]() ;
;
③![]() 的体积是
的体积是![]() ;
;
④平面![]() ⊥平面
⊥平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中正确的有 .(填写你认为正确的序号)
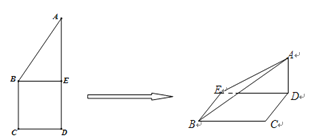
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com