
设a,b∈R,且a≠2,定义在区间(-b,b)内的函数f(x)=![]() 是奇函数.
是奇函数.
(1)求b的取值范围;
(2)讨论函数f(x)的单调性.
(1)b的取值范围是(0, ![]() ](2)f(x)在(-b,b)内是减函数,具有单调性.
](2)f(x)在(-b,b)内是减函数,具有单调性.
(1)f(x)=lg ![]() (-b<x<b)是奇函数等价于:
(-b<x<b)是奇函数等价于:
对任意x∈(-b,b)都有
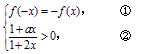 ①式即为=
①式即为=![]() ,由此可得
,由此可得
![]() ,也即a2x2=4x2,此式对任意x∈(-b,b)都成立相当于a2=4,因为a≠2,所以a=-2,代入②式,得
,也即a2x2=4x2,此式对任意x∈(-b,b)都成立相当于a2=4,因为a≠2,所以a=-2,代入②式,得![]() >0,即-
>0,即-![]() <x<
<x<![]() ,此式对任意x∈(-b,b)都成立相当于-
,此式对任意x∈(-b,b)都成立相当于-![]() ≤-b<b≤
≤-b<b≤![]() ,
,
所以b的取值范围是(0, ![]() ].
].
(2)设任意的x1,x2∈(-b,b),且x1<x2,
由b∈(0,![]() ],得-
],得-![]() ≤-b<x1<x2<b≤
≤-b<x1<x2<b≤![]() ,
,
所以0<1-2x2<1-2x1,0<1+2x1<1+2x2,
从而f(x2)-f(x1)= ![]()
因此f(x)在(-b,b)内是减函数,具有单调性.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
A.a,b,c全为正数 B.a,b,c全为非负实数
C.a+b+c≥0 D.a+b+c>0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练1练习卷(解析版) 题型:选择题
设a,b,c∈R,且a>b,则 ( )
(A)ac>bc (B)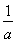 <
<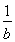
(C)a2>b2 (D)a3>b3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com