
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至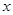 元,则本年度新增用电量
元,则本年度新增用电量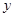 (亿千瓦时)与
(亿千瓦时)与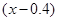 元成反比例.又当
元成反比例.又当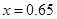 时,
时,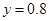 .
.
(1)求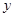 与
与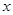 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益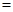 用电量
用电量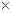 (实际电价-成本价)]
(实际电价-成本价)]
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为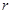 米,高为
米,高为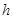 米,体积为
米,体积为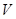 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为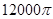 元(
元(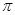 为圆周率).
为圆周率).
(1)将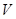 表示成
表示成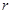 的函数
的函数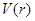 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数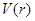 的单调性,并确定
的单调性,并确定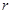 和
和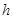 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lnx+a ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于x的一元二次函数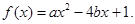
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和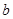 ,
,
求函数 在区间[
在区间[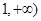 上是增函数的概率;
上是增函数的概率;
(2)设点( ,
,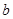 )是区域
)是区域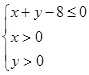 内的随机点,求函数
内的随机点,求函数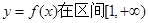 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com