
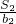
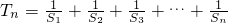 ,试比较Tn与
,试比较Tn与 的大小.
的大小. ,解之得,q=3或q=-4(负值舍去),a2=6
,解之得,q=3或q=-4(负值舍去),a2=6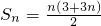 ,
,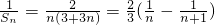
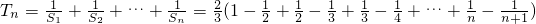
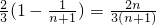 .
.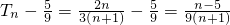
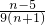 <0,得n<5,故 n=1,2,3,4;令
<0,得n<5,故 n=1,2,3,4;令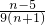 =0,得n=5;令
=0,得n=5;令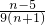 >0,得n>5
>0,得n>5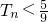 ;当n=5时,
;当n=5时,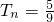 ;当 n>5(n∈N+)时,
;当 n>5(n∈N+)时,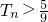 .
.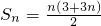 ,从而化简出
,从而化简出 ,用裂项法求出Tn=
,用裂项法求出Tn=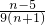 ,最后根据n与5的大小关系进行讨论,即可得到Tn与
,最后根据n与5的大小关系进行讨论,即可得到Tn与 的大小的几种情况.
的大小的几种情况. 的大小.着重考查了等差数列、等比数列的通项公式与求和公式,以及用不等式比较大小等知识,属于中档题.
的大小.着重考查了等差数列、等比数列的通项公式与求和公式,以及用不等式比较大小等知识,属于中档题. 

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com