
【题目】设函数![]()
![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)设![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(3)斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]()
![]() 两点,
两点,
求证:![]()
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上是增函数;当
上是增函数;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在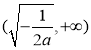 上单调递减;(3)见解析.
上单调递减;(3)见解析.
【解析】
(1)对函数![]() 求导,求其单调区间,即可求出极值,可得最小值;(2)分别讨论
求导,求其单调区间,即可求出极值,可得最小值;(2)分别讨论![]() 和
和![]() 时函数
时函数![]() 的单调性;(3)将直线斜率
的单调性;(3)将直线斜率![]() 用
用![]() 表示出来,将要证的不等式转化为证
表示出来,将要证的不等式转化为证![]() (
(![]() ),最后讨论函数
),最后讨论函数![]() (
(![]() )和
)和![]() (
(![]() )单调性,即可证明原题.
)单调性,即可证明原题.
(1)![]() ,令
,令![]() ,得
,得![]()
因为当![]() 时
时![]() ;当
;当![]() 时
时![]() ,
,
所以当![]() 时,
时,![]()
(2)![]() ,
,![]()
①当![]() 时,恒有
时,恒有![]() ,
,![]() 在
在![]() 上是增函数;
上是增函数;
②当![]() 时,
时,
令![]() ,得
,得![]() ,解得
,解得![]() ;
;
令![]() ,得
,得![]() ,解得
,解得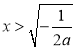 ,
,
综上,当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在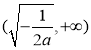 上单调递减
上单调递减
(3) ![]() .
.
要证![]() ,即证
,即证![]() ,等价于证
,等价于证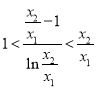 ,令
,令![]() ,
,
则只要证![]() ,由
,由![]() 知
知![]() ,故等价于证
,故等价于证![]() (*).
(*).
① 设![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是增函数,
上是增函数,
∴ 当![]() 时,
时,![]() ,即
,即![]() .
.
② 设![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是增函数,
上是增函数,
∴ 当![]() 时,
时,![]() ,即
,即![]() .
.
由①②知(*)成立,![]() 得证.
得证.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
【题目】类比平面几何中的定理:△ABC中,若DE是△ABC的中位线,则有S△ADE∶S△ABC=1∶4;若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为区间
的定义域为区间![]() ,若对于
,若对于![]() 内任意
内任意![]() ,都有
,都有![]()
![]() 成立,则称函数
成立,则称函数![]() 是区间
是区间![]() 的“
的“![]() 函数”.
函数”.
(1)判断函数![]() (
(![]() )是否是“
)是否是“![]() 函数”?说明理由;
函数”?说明理由;
(2)已知![]() ,求证:函数
,求证:函数![]() (
(![]() )是“
)是“![]() 函数”;
函数”;
(3)设函数![]() 是
是![]() ,(
,(![]() )上的“
)上的“![]() 函数”,
函数”,![]() ,且存在
,且存在![]() 使得
使得![]() ,试探讨函数
,试探讨函数![]() 在区间
在区间![]() 上零点个数,并用图象作出简要的说明(结果不需要证明).
上零点个数,并用图象作出简要的说明(结果不需要证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
(1)画散点图;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2﹣alnx﹣bx(a>0).
(Ⅰ)若a=1,b=3,求函数y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)若f(x1)=f(x2)=0,且x1≠x2,证明:f′(![]() )>0.
)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A. 回归直线一定过样本中心![]()
B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D. 甲、乙两个模型的![]() 分别约为0.98和0.80,则模型乙的拟合效果更好
分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com