Question

【题目】“函数在区间上单调”是“函数在上有反函数”的( )

A.充分不必要条件B.必要不充分条件

C.充分必要条件D.既不充分又不必要条件

Answer 1

【答案】A

【解析】

“函数在区间上单调”“函数在上有反函数”，反之不成立．即可判断出结论

“函数在区间上单调”“函数在上有反函数”，下面给出证明：

若“函数在区间上单调”，设函数在区间上的值域为，任取，如果在中存在两个或多于两个的值与之对应，设其中的某两个为，且，即，但．

因为，所以 (或)．

由函数在区间上单调知： ，(或)，这与矛盾．因此在中有唯一的值与之对应．由反函数的定义知：

函数在区间上存在反函数．

反之“函数在上有反函数”则不一定有“函数在区间上单调”，例如：函数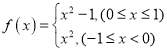，就存在反函数：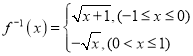

原函数和反函数图象分别如下图（1）（2）所示：

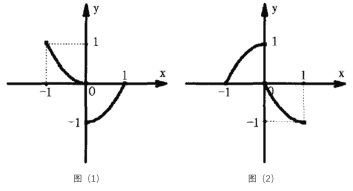
由图象可知：函数在区间上并不单调．

综上，“函数在区间上单调”是“函数在上有反函数”的充分不必要条件.

故选：A．