
����Ŀ��ij�����������ڣ�ÿ������10��ij��Ʒ�����е�һ��ڶ���ֱ�������1��2����Ʒ�����ʼ첿ÿ��Ҫ��������10����Ʒ�������ȡ4�����м�飬�������д�Ʒ������IJ�Ʒ����ͨ��.
��1��������ȫ��ͨ�����ĸ��ʣ�
��2�������ڶԸó��������IJ�Ʒ�������ý����ƶȣ�����ȫ��ͨ����鷣300Ԫ��ͨ��1�죬2��ֱ�300Ԫ900Ԫ.��ô�ó������������ڵõ��������ѧ�����Ƕ���Ԫ��
���𰸡���1��![]() .��2��
.��2��![]() (Ԫ)
(Ԫ)
��������
��1��������ֱ�ɵõ�һ����ͨ�����ĸ��ʣ��ɶ����¼��ĸ��ʹ�ʽ�ɵã�
��2�������ý���Ϊ��Ԫ��������ȡֵΪ��300��300��900���ֱ�������ʿɵ���ѧ����.
��1�������ȡ4����Ʒ���м��������¼�������һ����9����Ʒ���ڶ�����8����Ʒ��
��һ��ͨ�����ĸ���Ϊ![]() .
.
�ڶ���ͨ�����ĸ���Ϊ![]() .
.
��Ϊ��һ��ڶ������Ƿ�ͨ����������ģ�
��������ȫ��ͨ�����ĸ���Ϊ![]() .
.
��2�������ý���Ϊ��Ԫ��������ȡֵΪ��300��300��900 ��
������ɵ�![]() ��
��
![]() .
.
��![]() (Ԫ).
(Ԫ).


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�о�����������������в��ĸо�������������ǿ��![]() ��λ����
��λ����![]() ƽ����
ƽ����![]() �й�
�й�![]() ��ʵ�ʲ���ʱ������
��ʵ�ʲ���ʱ������![]() ��λ���ֱ�
��λ���ֱ�![]() ����ʾ����ǿ���ĵȼ�������������ǿ��I�����ϵʽ��
����ʾ����ǿ���ĵȼ�������������ǿ��I�����ϵʽ��![]() �dz���
�dz���![]() ������
������![]() ��
��![]() ƽ����
ƽ����![]() ��紵��Ҷɳɳ����ǿ��
��紵��Ҷɳɳ����ǿ��![]() ��
��![]() ƽ���ף�����ǿ���ȼ�
ƽ���ף�����ǿ���ȼ�![]() �ֱ���
�ֱ���
![]() ��֪�����м���������ǿ�������
��֪�����м���������ǿ�������
������Դ
������С | �紵��Ҷɳɳ�� | �������� | �����ӵ���· |
ǿ�� |
|
|
|
ǿ���ȼ� | 10 | m | 90 |
��a��m��ֵ
![]() Ϊ�˲�Ӱ����������Ϣ��˯�ߣ�������ǿ���ȼ�һ�㲻�ܳ���50�ֱ������ʱ����ǿ��I�����ֵ��
Ϊ�˲�Ӱ����������Ϣ��˯�ߣ�������ǿ���ȼ�һ�㲻�ܳ���50�ֱ������ʱ����ǿ��I�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������
������![]() �ϵ������ǡ�����
�ϵ������ǡ�����![]() ��
��![]() �����������( )
�����������( )
A.��ֲ���Ҫ����B.��Ҫ���������
C.��ֱ�Ҫ����D.�Ȳ�����ֲ���Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ķ�����Ϊ����
�Ķ�����Ϊ����![]() ��������
��������![]() ������
������![]() ������
������![]()
![]() ��������ƺ���
��������ƺ���![]() ������
������![]() �ġ�
�ġ�![]() ������.
������.
��1���жϺ���![]() ��
��![]() ���Ƿ��ǡ�
���Ƿ��ǡ�![]() ��������˵�����ɣ�
��������˵�����ɣ�
��2����֪![]() ����֤������
����֤������![]() ��
��![]() ���ǡ�
���ǡ�![]() ��������
��������
��3���躯��![]() ��
��![]() ,��
,��![]() ���ϵġ�
���ϵġ�![]() ��������
��������![]() ���Ҵ���
���Ҵ���![]() ʹ��
ʹ��![]() ����̽�ֺ���
����̽�ֺ���![]() ������
������![]() ��������������ͼ��������Ҫ��˵�����������Ҫ֤����.
��������������ͼ��������Ҫ��˵�����������Ҫ֤����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ̨����ʹ�õ�ʱ��ϳ�����������ʹ�ã�������ͬ��ת������������ij��е�����һЩ����ȱ�㣬ÿСʱ������ȱ������Ķ��٣����������ת���ٶȶ��仯���±�Ϊ��������Ľ����
ת��x(ת/��) | 2 | 4 | 5 | 6 | 8 |
ÿСʱ������ȱ��������y(��) | 30 | 40 | 60 | 50 | 70 |
��1����ɢ��ͼ��
��2�����y��x��������ع�ϵ����ع�ֱ�߷��̣�
��3����ʵ�������У�����ÿСʱ�IJ�Ʒ����ȱ���������Ϊ89������ô��������ת�ٶ�Ӧ������ʲô��Χ�ڣ�(�ο���ֵ��![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����(1)���һ����ѧ���Գɼ��ľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���ܵ���ͬ�̶ȵ��ƻ����ɼ��������£�

�Ը���ͼ���е���Ϣ����������⣺
(1)��ȫ���ѧ��������������[70,80)֮���Ƶ����
(2)Ϊ�����˽�ѧ���Ĵ����������ʦ���ֲ�����ķ�����λ��[70,80)��[80,90)��[90,100]�����ε��Ծ��г�ȡ8�ݽ��з������ٴ�����ѡ3�˽��н�����������ѧ���У��ɼ�λ��[70,80)�����ε�����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����x2+2��alnx��bx��a��0����
������a��1��b��3������y��f��x���ڣ�1��f��1�����������߷��̣�
������f��x1����f��x2����0����x1��x2��֤����f�䣨![]() ����0��
����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������ŮԱ��500�ˣ��ִ��г�ȡ100λԱ��������ÿ����ɺϸ��Ʒ�ļ���ͳ�����£�
ÿ����ɺϸ��Ʒ�ļ�������λ���ټ��� |
|
|
|
|
|
Ƶ�� | 10 | 45 | 35 | 6 | 4 |
��Ա������ | 7 | 23 | 18 | 1 | 1 |
��1������ÿ����ɺϸ��Ʒ�ļ���������3200����Ա������Ϊ���������֡�.������ͳ��������д����![]() �����������ж��Ƿ���95%�İ�����Ϊ���������֡����Ա��йأ�
�����������ж��Ƿ���95%�İ�����Ϊ���������֡����Ա��йأ�
�ǡ��������֡� | ���������֡� | �ϼ� | |
��Ա�� | |||
ŮԱ�� | |||
�ϼ� |
��2��Ϊ���Ա���Ͷ��Ļ����ԣ�����ʵ���۽��Ƽ������ƣ��涨ÿ����ɺϸ��Ʒ�ļ����ڶ���2600�����ڵģ��Ƽ�����Ϊ1Ԫ������![]() ���IJ��֣��۽��Ƽ�����Ϊ1.2Ԫ������
���IJ��֣��۽��Ƽ�����Ϊ1.2Ԫ������![]() ���IJ��֣��۽��Ƽ�����Ϊ1.3Ԫ������400�����ϵIJ��֣��۽��Ƽ�����Ϊ1.4Ԫ.����4���и��ε�Ƶ����Ϊ��Ӧ�ĸ��ʣ��ڸó���Ա����ѡȡ1�ˣ�ŮԱ�������ѡȡ2�˽��й��ʵ��飬��ʵ�üƼ����ʣ�ʵ�üƼ�����=����Ƽ�����+������Ƽ����ʣ�������3100Ԫ������Ϊ����ķֲ��к���ѧ����.
���IJ��֣��۽��Ƽ�����Ϊ1.3Ԫ������400�����ϵIJ��֣��۽��Ƽ�����Ϊ1.4Ԫ.����4���и��ε�Ƶ����Ϊ��Ӧ�ĸ��ʣ��ڸó���Ա����ѡȡ1�ˣ�ŮԱ�������ѡȡ2�˽��й��ʵ��飬��ʵ�üƼ����ʣ�ʵ�üƼ�����=����Ƽ�����+������Ƽ����ʣ�������3100Ԫ������Ϊ����ķֲ��к���ѧ����.
����![]() ��
��
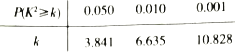 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Ӹ�һ�꼶ѧ���������ȡ60��ѧ���������п��Ե������ɼ�����Ϊ�������ֳ����Σ�![]() ��
��![]() ��
��![]() ������
������![]() ��õ���ͼƵ�ʷֲ�ֱ��ͼ.
��õ���ͼƵ�ʷֲ�ֱ��ͼ.
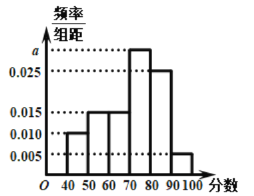
��1������Ƶ�ʷֲ�ֱ��ͼ��������������λ����
��2���÷ֲ�����ķ�����![]() ��ѧ���г�ȡһ������Ϊ5��������������������ѡ���˲μӲ������������˵ķ�������һ������
��ѧ���г�ȡһ������Ϊ5��������������������ѡ���˲μӲ������������˵ķ�������һ������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com