
【题目】已知函数f(x)=x2+2﹣alnx﹣bx(a>0).
(Ⅰ)若a=1,b=3,求函数y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)若f(x1)=f(x2)=0,且x1≠x2,证明:f′(![]() )>0.
)>0.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(Ⅰ)求f(x)的导数,可得切线的斜率,以及切点,由点斜式方程可得切线方程;
(Ⅱ)由函数零点定义,两方程相减可得两个零点之间的关系,用变量集中的方法,把两个零点集中为一个变量,求导数,判断单调性,即可得证..
解:(Ⅰ)若a=1,b=3,f(x)=x2+2﹣lnx﹣3x,
导数为f′(x)=2x﹣![]() ﹣3,
﹣3,
可得在x=1处切线的斜率为﹣2,
f(1)=0,可得切线方程为y=﹣2(x﹣1),
即为2x+y﹣2=0;
(Ⅱ)证明:若f(x1)=f(x2)=0,且x1≠x2,
可得x12+2﹣alnx1﹣bx1=0,x22+2﹣alnx2﹣bx2=0,
两式相减可得(x1﹣x2)(x1+x2)﹣a(lnx1﹣lnx2)﹣b(x1﹣x2)=0,
即有x1+x2﹣b=a![]() ,
,
可设x0=![]() ,
,
由f′(x0)=2x0﹣![]() ﹣b=(x1+x2﹣b)﹣
﹣b=(x1+x2﹣b)﹣![]()
=a![]() ﹣
﹣![]()
=![]() [ln
[ln![]() ﹣
﹣![]() ]
]
=![]() [ln
[ln![]() ﹣
﹣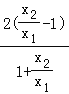 ],
],
令t=![]() ,t>1,可得f′(x0)=
,t>1,可得f′(x0)=![]() [lnt﹣
[lnt﹣![]() ],
],
设u(t)=lnt﹣![]() ,t>1,
,t>1,
导数为u′(t)=![]() ﹣
﹣![]() =
=![]() >0,
>0,
可得u(t)在t>1递增,且u(1)=0,
可得u(t)>u(1)=0,
即lnt﹣![]() >0,
>0,
又a>0,x2﹣x1>0,可得f′(x0)>0,
综上可得f′(![]() )>0.
)>0.


科目:高中数学 来源: 题型:
【题目】某车间在两天内,每天生产10件某产品,其中第一天第二天分别生产了1件2件次品,而质检部每天要在生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(1)求两天全部通过检查的概率;
(2)若厂内对该车间生产的产品质量采用奖惩制度,两天全不通过检查罚300元,通过1天,2天分别奖300元900元.那么该车间在这两天内得到奖金的数学期望是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
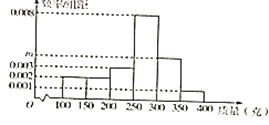
【题目】炎炎夏季,水蜜桃成为备受大家欢迎的一种水果,某果园的水蜜桃质量分布如图所示.
(Ⅰ)求m的值;
(Ⅱ)以频率估计概率,若从该果园中随机采摘5个水蜜桃,记质量在300克以上(含300克)的个数为X,求X的分布列及数学期望;
(Ⅲ)经市场调查,该种水蜜桃在过去50天的销售量(单位:千克)和价格(单位:元/千克)均为销售时间t(天)的函数,且销售量近似地满足f(t)=﹣3t+300(1≤t≤50,t∈N),前30天价格为g(t)=![]() +20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
+20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
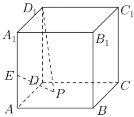
【题目】如图,正方体![]() 是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知
是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知![]() 为柱
为柱![]() 上一点(不在点
上一点(不在点![]() 、
、![]() 处),
处),![]() (
(![]() ),菜农需要在地面正方形
),菜农需要在地面正方形![]() 内画出一条曲线
内画出一条曲线![]() 将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点
将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点![]() 为地面正方形
为地面正方形![]() 内的曲线
内的曲线![]() 上任意一点,设
上任意一点,设![]() 、
、![]() 分别为在
分别为在![]() 点处观测
点处观测![]() 和
和![]() 的仰角.
的仰角.
(1)若![]() ,请说明曲线
,请说明曲线![]() 是何种曲线,为什么?
是何种曲线,为什么?
(2)若![]() 为柱
为柱![]() 的中点,且
的中点,且![]() 时,请求出点
时,请求出点![]() 所在区域的面积.
所在区域的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若给定非零实数
,若给定非零实数![]() ,对于任意实数
,对于任意实数![]() ,总存在非零常数
,总存在非零常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 是
是![]() 上的
上的![]() 级
级![]() 类周期函数,若函数
类周期函数,若函数![]() 是
是![]() 上的2级2类周期函数,且当
上的2级2类周期函数,且当![]() 时,
时,![]() ,又函数
,又函数![]() .若
.若![]() ,
,![]() ,使
,使![]() 成立,则实数
成立,则实数![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
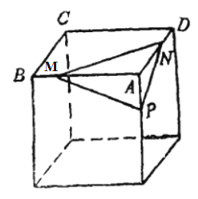
【题目】如图,设P、M、N分别是正方体的棱![]() ,AD,AB上非顶点的任意点.
,AD,AB上非顶点的任意点.
①![]() 的外心必在
的外心必在![]() 的某一边上;
的某一边上;
②![]() 的外心必在
的外心必在![]() 的内部;
的内部;
③![]() 的垂心必是点A在平面PMN上的射影;
的垂心必是点A在平面PMN上的射影;
④若线段AP、AM、AN的长分别为a、b、c,则![]() .其中( ).
.其中( ).
A. 只有①、④正确.
B. 只有③、④正确.
C. 只有②、③、④正确.
D. 只有②、③正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com