
(本题分12分)
定义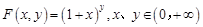 .
.
(Ⅰ)求曲线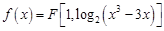 与直线
与直线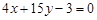 垂直的切线方程;
垂直的切线方程;
(Ⅱ)若存在实数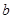 使曲线
使曲线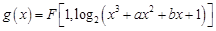 在
在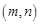 点处的切线斜率为
点处的切线斜率为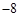 ,且
,且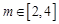 ,求实数
,求实数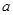 的取值范围.
的取值范围.
(1)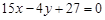 . (2)
. (2) 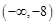 。
。
【解析】本试题主要是考查了导数的几何意义的运用,以及运用导数求解函数的最值问题的综合运用。
(1)因为所求曲线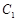 的切线与直线
的切线与直线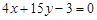 垂直,故令
垂直,故令
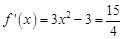 得
得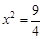 得到
得到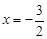 ,进而得到切线方程。
,进而得到切线方程。
(2)函数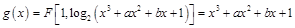
令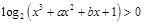 ,得
,得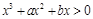
因切点为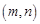 ,故有
,故有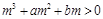 ,构造函数利用导数求解不等式转化为
,构造函数利用导数求解不等式转化为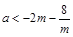 在
在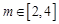 上有解来解决。
上有解来解决。
解:(1)函数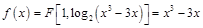 ,
,
依题意令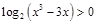 ①, -------------------------2分
①, -------------------------2分
因为所求曲线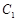 的切线与直线
的切线与直线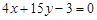 垂直,故令
垂直,故令
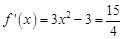 得
得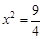 ②,由①②知应取
②,由①②知应取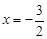 ,得
,得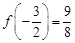 ,切点为
,切点为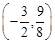 ,
,
所求切线方程是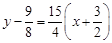 ,即
,即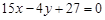 .------------------4分
.------------------4分
(2)函数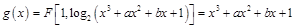
令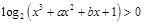 ,得
,得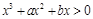
因切点为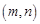 ,故有
,故有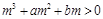 -----------------6分
-----------------6分
又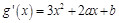 ,依题意有
,依题意有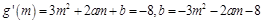
所以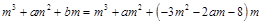
即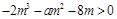 ---------------------8分
---------------------8分
该不等式在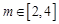 上有解,即
上有解,即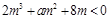 在
在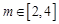 上有解,
上有解,
转化为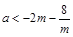 在
在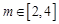 上有解,-------- -------------10分
上有解,-------- -------------10分
令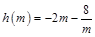 ,则
,则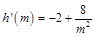 ,在
,在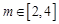 上恒有
上恒有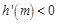
所以函数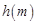 是
是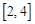 上的减函数,
上的减函数,
其最大值为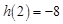 ,所以实数
,所以实数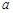 的取值范围是
的取值范围是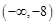 --------------12分
--------------12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012届湖南省衡阳市八中高三上学期第一次月考理科数学 题型:解答题
(本题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:
| 付款方式 | 分l期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
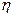 表示经销一辆汽车的利润
表示经销一辆汽车的利润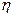 的分布列及数学期望
的分布列及数学期望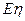
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省高三上学期开学考试理科数学试卷(解析版) 题型:解答题
(本题分12分)
如图,斜率为1的直线过抛物线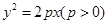 的焦点,与抛物线交于两点A、B, 将直线
的焦点,与抛物线交于两点A、B, 将直线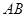 按向量
按向量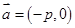 平移得到直线
平移得到直线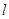 ,
,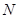 为
为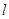 上的动点,
上的动点,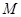 为抛物线弧
为抛物线弧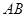 上的动点.
上的动点.
(Ⅰ)
若 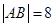 ,求抛物线方程.
,求抛物线方程.
(Ⅱ)求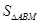 的最大值.
的最大值.
(Ⅲ)求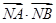 的最小值.
的最小值.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省高三上学期开学考试理科数学试卷(解析版) 题型:解答题
(本题分12分)
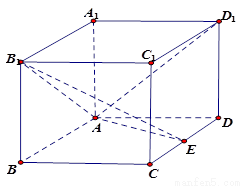
如图,在长方体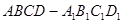 中,
中,
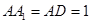 ,
,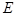 为
为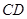 中点.
中点.
(Ⅰ)求证: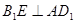 ;
;
(Ⅱ)在棱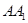 上是否存在一点
上是否存在一点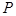 ,使得
,使得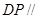 平面
平面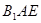 ?若存在,求
?若存在,求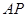 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(Ⅲ)若二面角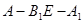 的大小为
的大小为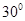 ,求
,求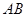 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省长、望、浏、宁高三3月一模联考理科数学试卷 题型:解答题
(本题满分12分)
在某次考试中共有12道选择题,每道选择题有4个选项,其中只有一个是正确的,评分标准规定:“每题只选一项,答对得5分,不答或答错得0分”。某考生每道题给出一个答案,并已确定有9道题的答案是正确的,而其余题中,有一道题可判断出两个选项是错误的,有一道题可以判断出一个选项是错误的,还有一道题因不了解题意只能乱猜,试求出该考生;
(1)选择题得60分的概率;
(2)选择题所得分数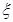 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源:安徽省2010届高三第三次模拟考试数学(文)试卷 题型:解答题
(本题满分12分)某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学 成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理 成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
|
|
数学成绩优秀 |
数学成绩不优秀 |
合 计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
|
|
|
合 计 |
|
|
20 |
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率.
参考数据及公式:
①随机变量 ,其中
,其中 为样本容量;
为样本容量;
②独立检验随机变量 的临界值参考表:
的临界值参考表:
|
|
0.010 |
0.005 |
0.001 |
|
|
6.635 |
7.879 |
10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com