
设不等式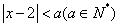 的解集为
的解集为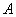 ,且
,且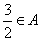 ,
,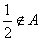 .
.
(1)求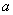 的值;
的值;
(2)求函数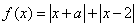 的最小值.
的最小值.
科目:高中数学 来源: 题型:
某班班会准备从含有甲、乙、丙的7名学生中选取4人发言,要求甲、乙两人至少有一人参加,若甲、乙同时参加时,丙不能参加,且甲、乙两人的发言顺序不能相邻,那么不同的发言顺序有
A.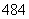 种 B.
种 B.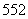 种 C.
种 C.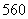 种 D.
种 D.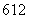 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点(1, )是函数
)是函数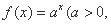 且
且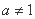 )的图象上一点,等比数列
)的图象上一点,等比数列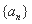 的前
的前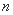 项和为
项和为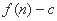 ,数列
,数列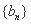
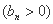 的首项为
的首项为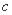 ,且前
,且前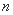 项和
项和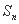 满足
满足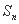 -
-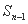 =
=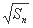 +
+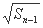 (
(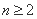 ).
).
(1)求常数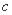 ;
;
(2)求数列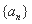 和
和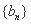 的通项公式;
的通项公式;
(3)若数列{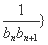 前
前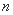 项和为
项和为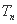 ,问
,问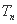
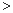
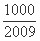 的最小正整数
的最小正整数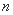 是多少?
是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com