
 处时获悉,在其正东方向相距20海里的
处时获悉,在其正东方向相距20海里的 处有一艘渔船遇险
处有一艘渔船遇险 等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里
,相距10海里 处的乙船.
处的乙船.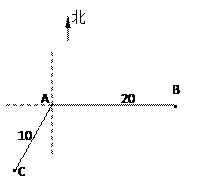
 处的乙船和遇险渔船间的距离;
处的乙船和遇险渔船间的距离;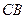 方向前往
方向前往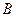 处救援,其方向与
处救援,其方向与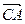 成
成 角,求
角,求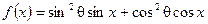
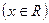 的值域.
的值域. 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:不详 题型:解答题
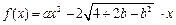 ,
,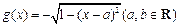 .
.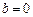 时,若
时,若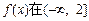 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;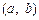 :存在
:存在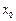 ,使得
,使得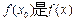 的最大值,
的最大值,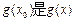 的最小值;
的最小值;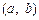 ,试构造一个定义在
,试构造一个定义在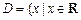 且
且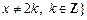 上的函数
上的函数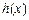 :使
:使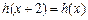 ,且当
,且当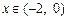 时,
时,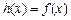 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
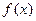 的图像恰好通过
的图像恰好通过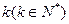 个格点,则称函数
个格点,则称函数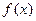 为k阶格点函数,下列函数中“一阶格点”函数有
为k阶格点函数,下列函数中“一阶格点”函数有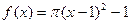 ②
②
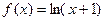 ④
④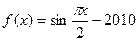
| A.②③ | B.①③ | C.①④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
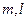 ,平面
,平面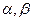 ,若
,若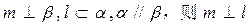
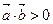 ,是
,是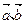 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;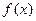 在
在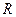 上满足
上满足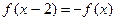 ,则
,则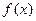 是以4为周期的周期函数;
是以4为周期的周期函数;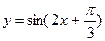 的图象的一个对称中心是(
的图象的一个对称中心是(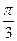 ,0);
,0);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com