
分析 设M(x,y),由MA=2MO,利用两点间的距离公式列出关系式,整理后得到点M的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,由M在圆C上,得到圆C与圆D相切,根据两圆的半径长,能求出结果.
解答 解:设点M(x,y),由MA=2MO,知:$\sqrt{{x}^{2}+(y-3)^{2}}$=2$\sqrt{{x}^{2}+{y}^{2}}$,
化简得:x2+(y+1)2=4,
∴点M的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D,
又∵点M在圆C上,圆C上存在唯一一点M,使|MA|=2|MO|,
∴圆C与圆D相切,
∴|CD|=1或CD=3,
∵|CD|=$\sqrt{{a}^{2}+(2a-3)^{2}}$,∴解得a=0或a=$\frac{12}{5}$.
∴圆心C的非零横坐标是$\frac{12}{5}$.
故答案为:$\frac{12}{5}$.
点评 此题考查了圆的切线方程,点到直线的距离公式,以及圆与圆的位置关系的判定,涉及的知识有:两直线的交点坐标,直线的点斜式方程,两点间的距离公式,圆的标准方程,是一道综合性较强的试题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
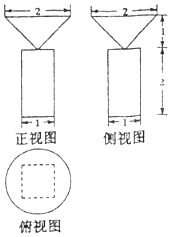
| A. | $\frac{π}{3}$+2 | B. | $\frac{π}{3}$+$\frac{2}{3}$ | C. | π$+\frac{2}{3}$ | D. | π+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+1 | B. | $\sqrt{6}$+$\sqrt{2}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{3}+$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com