
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
分析 根据题意,由函数的奇偶性以及f(2-x)=f(x)分析可得f(2+x)=-f(x),进而可得f(4+x)=f(x),则函数f(x)的周期为4;则f(2017)=f(5×504+1)=f(1)=-f(-1),由-1≤x<0时,函数的解析式计算可得答案.
解答 解:根据题意,f(x)是定义在R上的奇函数,且f(2-x)=f(x),
则有f(2+x)=-f(x),
则f(4+x)=f[2+(2+x)]=-f(2+x)=f(x),则函数f(x)的周期为4,
f(2017)=f(5×504+1)=f(1)=-f(-1)=-log2[(-3)×(-1)+1]=-2,
即f(2017)=-2;
故选:B.
点评 本题考查函数的奇偶性、周期性的应用,关键是求出该函数的周期.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移1个单位长度,再向上平移2个单位长度 | |
| B. | 向右平移1个单位长度,再向上平移2个单位长度 | |
| C. | 向左平移1个单位长度,再向下平移2个单位长度 | |
| D. | 向右平移1个单位长度,再向下平移2个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
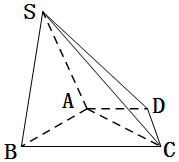 如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.
如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com