
【题目】已知二次函数f(x)的二次项系数为a,且f(x)>﹣x的解集为{x|1<x<2},方程f(x)+2a=0有两相等实根,求f(x)的解析式.
【答案】解:设f(x)=ax2+bx+c,由f(x)>﹣x,可得ax2+(b+1)x+c>0,∵f(x)>﹣x的解集为{x|1<x<2},
∴ 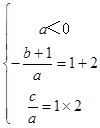 ,解得
,解得  ,
,
∴f(x)=ax2﹣(3a+1)x+2a.
∵f(x)+2a=0,即ax2﹣(3a+1)x+4a=0有两相等实根,
∴△=(3a+1)2﹣16a2=0,解得a=1舍去或 ![]() .④
.④
由①②③④得: ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]()
【解析】设f(x)=ax2+bx+c,由f(x)>﹣x,可得ax2+(b+1)x+c>0,由f(x)>﹣x的解集为{x|1<x<2},列出不等式组,求解即可得a,b,c的关系式,再由f(x)+2a=0求出a的值,结合a,b,c的关系式即可得答案.
【考点精析】掌握函数的定义域及其求法是解答本题的根本,需要知道求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】(Ⅰ)平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 过点
过点![]() ,以原点
,以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程(
的参数方程(![]() 为常数)和曲线
为常数)和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求倾斜角
,求倾斜角![]() 的值.
的值.
(Ⅱ)已知函数![]() .
.
(1)若函数![]() 的最小值为5,求实数
的最小值为5,求实数![]() 的值;
的值;
(2)求使得不等式![]() 成立的实数
成立的实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在平面直角坐标系中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ) 求曲线![]() 与
与![]() 交点的平面直角坐标;
交点的平面直角坐标;
(Ⅱ) 点![]() 分别在曲线
分别在曲线![]() ,
, ![]() 上,当
上,当![]() 最大时,求
最大时,求![]() 的面积(
的面积(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 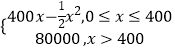 ,其中x是仪器的月产量.(注:总收益=总成本+利润)
,其中x是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润x表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.
(1)在图中画出过点![]() 的平面
的平面![]() ,使得
,使得![]() 平面
平面![]() (必须说明画法,不需证明);
(必须说明画法,不需证明);
(2)若二面角![]() 是
是![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的钢板的边界![]() 是抛物线的一部分,且
是抛物线的一部分,且![]() 垂直于抛物线对称轴,现欲从钢板上截取一块以
垂直于抛物线对称轴,现欲从钢板上截取一块以![]() 为下底边的等腰梯形钢板
为下底边的等腰梯形钢板![]() ,其中
,其中![]() 均在抛物线弧上.设
均在抛物线弧上.设![]() (米),且
(米),且![]() .
.
(1)当![]() 时,求等腰梯形钢板的面积;
时,求等腰梯形钢板的面积;
(2)当![]() 为何值时,等腰梯形钢板的面积最大?并求出最大值.
为何值时,等腰梯形钢板的面积最大?并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次函数f(x)是R上的增函数,已知f[f(x)]=16x+5,g(x)=f(x)(x+m).
(1)求f(x);
(2)若g(x)在(1,+∞)单调递增,求实数m的取值范围;
(3)当x∈[﹣1,3]时,g(x)有最大值13,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义在R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0<x<1},则A中所有元素之和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,定义x≥0时,f(x)= ![]()
(1)求f(﹣2);
(2)当x<﹣3时,求f(x)的解析式;
(3)设函数y=f(x)在区间[﹣5,5]上的最大值为g(a),试求g(a)的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com