
分析 (Ⅰ)当-2≤x≤3时,f(x)≤4成立,可得x-4≤a≤x+4,即可求实数a的取值范围;
(Ⅱ)存在实数x,使得f(x-a)-f(x+a)≤2a-1成立,转化为-2|a|≤2a-1,分类讨论,即可求实数a的取值范围.
解答 解:(Ⅰ)当-2≤x≤3时,f(x)≤4成立,即|x-a|≤4,
可得-4≤x-a≤4,
∴x-4≤a≤x+4,
∵-2≤x≤3,
∴-1≤a≤2; …(5分)
(Ⅱ)∵f(x-a)-f(x+a)≤2a-1成立,
∴-2|a|≤|x-2a|-|x|≤2|a|,
∵存在实数x,使得f(x-a)-f(x+a)≤2a-1成立,
∴-2|a|≤2a-1.
a≥0时,-2a≤2a-1,解得a≥$\frac{1}{4}$;
a<0时,2a≤2a-1,矛盾,舍去;
综上,a≥$\frac{1}{4}$ …(10分)
点评 本题考查绝对值不等式,考查存在性问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-3,-1)∪(3,+∞) | B. | (-3,-1)∪(2,+∞) | C. | (-3,+∞) | D. | (-∞,-3)(-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为4,15,26,37,48的同学均被选出,则该班学生人数可能为55 | |
| B. | “x<0”是“ln(x+1)<0”的必要不充分条件 | |
| C. | “?x≥2,x2-3x+2≥0”的否定是?x<2,x2-3x+2<0 | |
| D. | x<3是-1<x<3的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
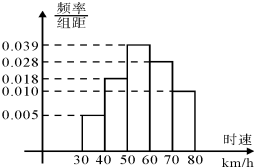 200辆汽车经过某一雷达地区,时速的频率分布直方图如图所示
200辆汽车经过某一雷达地区,时速的频率分布直方图如图所示 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com