设{an}(n∈N*)为等差数列,则使|a1|+|a2|+…+|an|=|a1+1|+|a2+1|+…+|an+1|=|a1+2|+|a2+2|+…+|an+2|=|a1+3|+|a2+3|+…+|an+3|=2010成立的数列{an}的项数n的最大值是________.
50
分析:根据等差数列|a
1|+|a
2|+…+|a
n|=|a
1+1|+|a
2+1|+…+|a
n+1|=|a
1+2|+|a
2+2|+…+|a
n+2|=|a
1+3|+|a
2+3|+…+|a
n+3|=2010,可得数列{a
n}中 的有正有负,不妨设
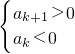
,根据题意可得d>3,根据|a
1|+|a
2|+…+|a
n|=2010,去绝对值求和,即可求得结果.
解答:{a
n}(n∈N
*)为等差数列,因为|a
1|+|a
2|+…+|a
n|=|a
1+1|+|a
2+1|+…+|a
n+1|=|a
1+2|+|a
2+2|+…+|a
n+2|=|a
1+3|+|a
2+3|+…+|a
n+3|,
∴{a
n}中的项一定满足
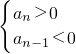
或

,
且项数n为偶数,设n=2k,k∈N
*,等差数列的公差为d,首项为a
1,不妨设
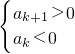
,
则a
1<0,d>0,且a
k+3<0,由
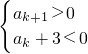
可得d>3,
∴|a
1|+|a
2|+…+|a
n|=-a
1-a
2-…-a
k+a
k+1+a
k+2+…+a
2k=-2(a
1+a
2+…+a
k)+(a
1+a
2+…+a
k+a
k+1+a
k+2+…+a
2k)
=-2[ka
1+

d]+2ka
1+
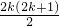
d=k
2d=2010,
∵d>3,
∴k
2d=2010>3k
2,解得k
2<670,而k∈N
*,
∴k≤25,故n≤50.
∴使|a
1|+|a
2|+…+|a
n|=|a
1+1|+|a
2+1|+…+|a
n+1|=|a
1+2|+|a
2+2|+…+|a
n+2|=|a
1+3|+|a
2+3|+…+|a
n+3|=2010成立的数列{a
n}的项数n的最大值是50.
故答案为:50.
点评:本题考查了等差数列的性质,根据题意求出数列的项的特点和公差的范围是解题的关键,属中档题.

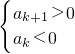 ,根据题意可得d>3,根据|a1|+|a2|+…+|an|=2010,去绝对值求和,即可求得结果.
,根据题意可得d>3,根据|a1|+|a2|+…+|an|=2010,去绝对值求和,即可求得结果.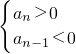 或
或 ,
,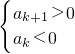 ,
,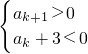 可得d>3,
可得d>3, d]+2ka1+
d]+2ka1+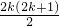 d=k2d=2010,
d=k2d=2010,
