[题目]若一个三位数的各位数字中.有且仅有两个数字一样.我们就把这样的三位数定义为“单重数 .例如:232.114等.则不超过200的“单重数中.从小到大排列第25个“单重数是( )A.166B.171C.181D.188 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】若一个三位数的各位数字中，有且仅有两个数字一样，我们就把这样的三位数定义为“单重数”.例如：232，114等，则不超过200的“单重数”中，从小到大排列第25个“单重数”是（）

A.166B.171C.181D.188

【答案】D

【解析】

根据题意，分2种情况求出200以内的“单重数”的个数为27，据此分析其中最大的“单重数”，即可得答案．

在符合条件的三位数中，有两个1且1在百位的有个.

1在首位但不是重复数字的有100，122，133，144，155，166，177，188，199，共9个，

则200以内的“单重数”有18+9=27个，

其中最大的为199，其次为191，188,则从小到大排列第25个“单重数”是188.

故选：D

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）求的单调性；

（2）若对定义域内任意的，都恒成立，求a的取值范围；

（3）记，若在区间内有2个零点，求a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将一颗质地均匀的正方体骰子（六个面的点数分别为1、2、3、4、5、6）先后抛掷两次，记第一次出现的点数为，第二次出现的点数为.

（1）设复数（为虚数单位），求事件“为实数”的概率；

（2）求点落在不等式组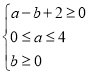表示的平面区域内（含边界）的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣，“放牧人粗心大意，三畜偷偷吃苗青，苗主扣住牛马羊，要求赔偿五斗粮，三畜户主愿赔偿，牛马羊吃得异样．马吃了牛的一半，羊吃了马的一半．”请问各畜赔多少？它的大意是放牧人放牧时粗心大意，牛、马、羊偷吃青苗，青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食（1斗=10升），三畜的主人同意赔偿，但牛、马、羊吃的青苗量各不相同．马吃的青苗是牛的一半，羊吃的青苗是马的一半．问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食？（）

A.B.C.D.