
已知函数 .
.
(1)当 时,求曲线
时,求曲线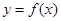 在点
在点 处的切线方程;
处的切线方程;
(2)当 ,且
,且 ,求函数
,求函数 的单调区间.
的单调区间.
(1) 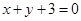 ;(2)当
;(2)当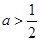 时,
时, 在
在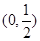 ,
,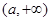 上单调递增,在
上单调递增,在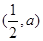 上单调递减,当
上单调递减,当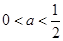 时,
时, 在
在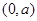 ,
,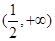 上单调递增,在
上单调递增,在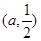 上单调递减.
上单调递减.
解析试题分析:本题综合考查函数与导数及运用导数求单调区间和切线方程等数学知识和方法,考查函数思想、分类讨论思想.第一问,先把 代入,得到
代入,得到 解析式,对它求导,将切点的横坐标代入得到切线的斜率,将1代入到
解析式,对它求导,将切点的横坐标代入得到切线的斜率,将1代入到 表达式中得到切点的纵坐标,最后通过点斜式方程直接写出切线方程;第二问,先对
表达式中得到切点的纵坐标,最后通过点斜式方程直接写出切线方程;第二问,先对 求导,令
求导,令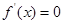 得到方程的2个根
得到方程的2个根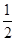 和
和 ,讨论
,讨论 和
和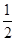 的大小,分情况令
的大小,分情况令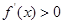 得函数的增区间,
得函数的增区间, 得函数的减区间.
得函数的减区间.
试题解析:(1)当 时,
时,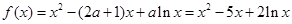 ,
,
∴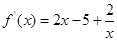 ,(2分)
,(2分)
∴ ,
,
又 ,(4分)
,(4分)
∴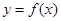 在点
在点 处的切线方程为
处的切线方程为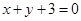 .(5分)
.(5分)
(2)  (
(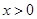 ),
),
令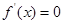 ,可得
,可得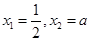 .(6分)
.(6分)
①当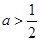 时,由
时,由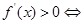
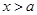 或
或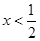 ,
, 在
在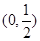 ,
,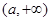 上单调递增.
上单调递增.
由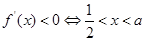 .
. 在
在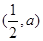 上单调递减.(9分)
上单调递减.(9分)
②当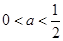 时,由
时,由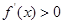 可得
可得 在
在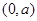 ,
,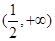 上单调递增.
上单调递增.
由 可得
可得 在
在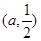 上单调递减.(12分)
上单调递减.(12分)
考点:1.利用导数求切线方程;2.利用导数求函数的单调区间.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com