
已知函数f(x)=ln -a
-a +x(a>0).
+x(a>0).
(Ⅰ)若 =
=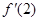 ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;
(Ⅱ)若 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.
(Ⅰ)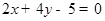 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)若 =
=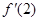 ,求
,求 图像在
图像在 处的切线的方程,须求
处的切线的方程,须求 图像在
图像在 处的切线的斜率,即
处的切线的斜率,即 的值,及
的值,及 的值,这样需求参数
的值,这样需求参数 的值,注意到条件
的值,注意到条件 ,可以建立方程来确定参数
,可以建立方程来确定参数 的值,本题思维简单,学生比较容易得分;(Ⅱ)证明:
的值,本题思维简单,学生比较容易得分;(Ⅱ)证明: ,需要求出
,需要求出 的极大值和极小值,但此题是字母,不能求出,可考虑它们的和的问题,可设极大值点,与极小值点分别为
的极大值和极小值,但此题是字母,不能求出,可考虑它们的和的问题,可设极大值点,与极小值点分别为 ,利用根与系数关系,得
,利用根与系数关系,得 ,这样
,这样 就转化为关于参数
就转化为关于参数 的关系式,利用导数求出
的关系式,利用导数求出 的单调性,从而证出,此题出题新颖,构思巧妙,确实是一个好题.
的单调性,从而证出,此题出题新颖,构思巧妙,确实是一个好题.
试题解析:(Ⅰ)
 ,
, ,即
,即
 ,
, ,
,
 图像在
图像在 处的切线的方程为
处的切线的方程为 ,即
,即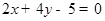 ;
;
(Ⅱ)设 为方程
为方程 的两个实数根,则
的两个实数根,则 ,由题意得:
,由题意得:  ,
, ,
,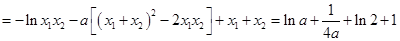 ,令
,令 ,则
,则 ,
, 时,
时,
 是减函数,则
是减函数,则
即 .
.
考点:本题考查函数与导数,导数与函数的单调性、导数与函数的极值,曲线的切线方程,导数与不等式的综合应用,考查学生的基本推理能力,考查学生的基本运算能力以及转化与化归的能力.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知函数 ,(其中m为常数).
,(其中m为常数).
(1) 试讨论 在区间
在区间 上的单调性;
上的单调性;
(2) 令函数 .当
.当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 、
、 ,使得过
,使得过 、
、 点处的切线互相平行,求
点处的切线互相平行,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,设曲线
,设曲线 在与
在与 轴交点处的切线为
轴交点处的切线为 ,
, 为
为 的导函数,满足
的导函数,满足 .
.
(1)求 ;
;
(2)设 ,
, ,求函数
,求函数 在
在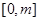 上的最大值;
上的最大值;
(3)设 ,若对于一切
,若对于一切 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 在
在 的延长线上,
的延长线上, 在
在 的延长线上,且对角线
的延长线上,且对角线 过
过 点.已知
点.已知 米,
米, 米。
米。
(1)设 (单位:米),要使花坛
(单位:米),要使花坛 的面积大于32平方米,求
的面积大于32平方米,求 的取值范围;
的取值范围;
(2)若 (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为
处的切线斜率为 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,求函数 的单调区间;
的单调区间;
(3)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com