
分析 (1)化简集合B,分类讨论,利用A∩B=∅,求a的取值范围;
(2)根据条件A∪B=R,确定不等式端点之间的关系进行求解即可.
解答 解:B={x|(x-1)(x-5)>0}={x|x<1或x>5},…(1分)
(1)当A=∅时,2a>a+3,∴a>3,…(2分)
当A≠∅时,$\left\{{\begin{array}{l}{2a≤a+3}\\ \begin{array}{l}2a≥1\\ a+3≤5\end{array}\end{array}}\right.$,∴$\frac{1}{2}≤a≤2$.…(5分)
综上,a的取值范围为$[{\frac{1}{2},2}]∪({3,+∞})$.…(6分)
(2)假设存在a使A∪B=R,则$\left\{\begin{array}{l}{2a≤1}\\{a+3≥5}\end{array}\right.$,…(8分)
∴a∈∅,∴不存在a使A∪B=R. …(10分)
点评 本题主要考查集合的基本运算,根据不等式的解法是解决本题的关键.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
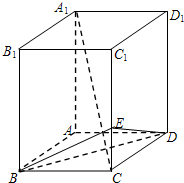 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 7.5 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)
如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=0 | B. | a≥$\frac{9}{8}$ | C. | a=0或a≥$\frac{9}{8}$ | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com