
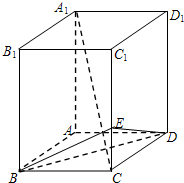
 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$. 分析 (1)通过VC-BDE=VE-BCD,直接求解几何体的体积即可.
(2)以点A为原点,AB、AD、AA1所在直线分别为x轴、y轴和z轴,建立空间直角坐标系,求出相关点的坐标,利用斜率垂直数量积为0,证明A1C⊥BE,A1C⊥BD,即可证明A1C⊥平面BDE,然后求解直线CC1与平面BDE所成角的正弦值.
解答 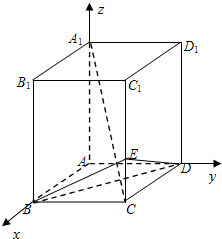 解:(1)由$CE=\frac{1}{4}C{C_1}$=$\frac{1}{2}$,
解:(1)由$CE=\frac{1}{4}C{C_1}$=$\frac{1}{2}$,
∴VC-BDE=VE-BCD…(2分)
=$\frac{1}{3}{S_{△BCD}}•CE=\frac{1}{3}×\frac{1}{2}×1×1×\frac{1}{2}=\frac{1}{12}$.…(6分)
(2)以点A为原点,AB、AD、AA1所在直线分别为x轴、y轴和z轴,建立空间直角坐标系,则$B({1,0,0})、D({0,1,0})、E({1,1,\frac{1}{2}})、{A_1}({0,0,2})、C({1,1,0})$,
∴$\overrightarrow{{A_1}C}=({1,1,-2})$,$\overrightarrow{BD}=({-1,1,0}),\overrightarrow{BE}=({0,1,\frac{1}{2}})$. …(8分)
∵$\overrightarrow{{A_1}C}•\overrightarrow{BD}=({1,1,-2})•({-1,1,0})=1×({-1})+1×1+({-2})×0=0$,$\overrightarrow{{A_1}C}•\overrightarrow{BE}=({1,1,-2})•({0,1,\frac{1}{2}})=1×0+1×1+({-2})×\frac{1}{2}=0$,…(10分)
∴$\overrightarrow{{A_1}C}⊥\overrightarrow{BD},\overrightarrow{{A_1}C}⊥\overrightarrow{BE}$.
∴A1C⊥BE,A1C⊥BD.
∵BE∩BD=B,BE?平面BDE,ED?平面BDE,
∴A1C⊥平面BDE. …(12分)
直线CC1与平面BDE所成角的余弦值:cosθ=|$\frac{\overrightarrow{{A}_{1}C}•\overrightarrow{{CC}_{1}}}{\overrightarrow{|{A}_{1}C}|•|\overrightarrow{{CC}_{1}}|}$|=$\frac{4}{2×\sqrt{1+1+4}}$=$\frac{2}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$.
直线CC1与平面BDE所成角的正弦值:$\frac{\sqrt{3}}{3}$.…(14分)
点评 本题考查直线与平面所成角的求法,直线与平面垂直的判断,几何体的求解的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (a,d)∪(b,c) | B. | (c,a]∪[b,d) | C. | (a,c]∪[d,b) | D. | (c,a)∪(d,b) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | -p | D. | (-p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | [0,2]∪{3} | C. | [0,+∞) | D. | [-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$<$\frac{f(1)}{f(2)}$<$\frac{1}{8}$ | B. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | C. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{3}$ | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com