
| A. | p∧q | B. | p∨q | C. | -p | D. | (-p)∨q |
分析 分别判断出p,q的真假,从而判断出复合命题的真假即可.
解答 解:关于命题p:函数f(x)=sinxcosx=$\frac{1}{2}$sin2x,
由2kπ-$\frac{π}{2}$<2x<2kπ+$\frac{π}{2}$,解得:kπ-$\frac{π}{4}$<x<kπ+$\frac{π}{4}$,
故f(x)的单调递增区间[$kπ-\frac{π}{4}$,$kπ+\frac{π}{4}$](k∈Z),
命题p是真命题;
关于命题q:函数g(x)=sin(x+$\frac{π}{2}$)的图象关于(-$\frac{π}{2}$,0)对称,
故关于关于原点对称错误,
故命题q是假命题;
故p∨q是真命题,
故选:B.
点评 本题考查了复合命题的真假,考查三角函数问题,是一道基础题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2016)<0 | B. | f(2016)<e${\;}^{-201{6}^{2}}$ | ||
| C. | f(2)<0 | D. | f(2)>e-4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
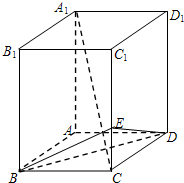 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,E是棱CC1上的点,且$CE=\frac{1}{4}C{C_1}$. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
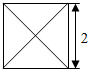 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 7.5 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com