
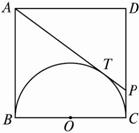
图2-14
思路分析:注意到AB、AT为切线,PT、PC为切线,则想到连结OA、OT、OP,构造切线长定理的基本图形,要求AT∶TP,则只需求AB∶PC,这可以通过解直角三角形或△ABO∽△OCP求得.
解法一:连结AO、TO、OP.?
∵四边形ABCD为正方形,?
∴BC⊥AB,BC⊥CD.?
又∵BC为⊙O的直径,?
∴AB、DC为⊙O的切线,切点为B、C.?
∵AT、AB切⊙O于T、B,?
∴AT =AB且∠AOB =∠AOT.?
∵PT、PC切⊙O于T、C,?
∴PT =PC且∠POT =∠POC.?
又∵∠AOB +∠AOT +∠POT +∠POC =180°,?
∴∠AOB +∠POC =∠AOP =90°.?
又∠ABO =90°,∴∠POC=∠BAO.?
∴Rt△ABO∽△Rt△OCP.∴![]() =
=![]() =
=![]() .?
.?
∴OB =2CP.∴AB =2OC =2OB =4CP,?
即AT∶TP =4∶1.
解法二:先证得∠BAO =∠POC(方法同上).?
在Rt△ABO中,tan∠BAO =![]() =
=![]() ,?
,?
在Rt△OCP中,PC =OC·tan∠POC =![]() =
=![]() ×
×![]() =
=![]() ,?
,?
∴AT∶TP =4∶1.
解法三:先证得AT =AB,PT =PC(方法同上).?
设正方形边长为a,PT =PC =x,则PD =a-x.?
又∵AT =AB =AD =a,在Rt△ADP中,AD2+DP2 =AP2,?
即a2+(a -x)2=(a +x)2,解得![]() .?
.?
∴AT∶TP =4∶1.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:
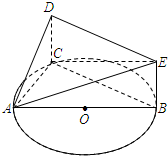 (2013•江门一模)如图,AB是圆O的直径,C是圆O上除A、B外的一点,△AED在平面ABC的投影恰好是△ABC.已知CD=BE,AB=4,tan∠EAB=
(2013•江门一模)如图,AB是圆O的直径,C是圆O上除A、B外的一点,△AED在平面ABC的投影恰好是△ABC.已知CD=BE,AB=4,tan∠EAB=| 1 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
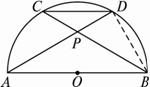
图2-1-14
A.sin∠BPD B.cos∠BPD C.tan∠BPD D.cot∠BPD
查看答案和解析>>
科目:高中数学 来源: 题型:
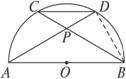
图2-1-14
A.sin∠BPD B.cos∠BPD
C.tan∠BPD D.cot∠BPD
查看答案和解析>>
科目:高中数学 来源: 题型:
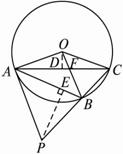
图2-3-14
(1)求弦AC、AB的长;
(2)若P为CB延长线上的一点,试确定P点的位置,使得PA与⊙O相切,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com