
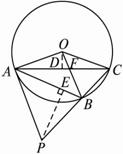
图2-3-14
(1)求弦AC、AB的长;
(2)若P为CB延长线上的一点,试确定P点的位置,使得PA与⊙O相切,并证明你的结论.
思路分析:(1)要求AC,可在△AOC中求解,求AB,可在△AOB中求解.?
(2)要确定P的位置,只需求PB,可在△APB中求解,过P作PE⊥AB,则将斜三角形分解为直角三角形.

解:(1)过O作OD⊥AC于D,?
∵∠ABC=120°,则∠AOC=120°.?
又OA =OC,?
∴∠OAD =∠OCD=30°.?
在Rt△AOD中,cos∠OAD =![]() ,又OA =1,?
,又OA =1,?
∴AD =OA·cos30°=![]() .∴AC =2AD =
.∴AC =2AD =![]() .?
.?
在△AOB中,OA =OB =1,∠AOB =2∠ACB =90°,∴![]() .?
.?
(2)过P作PE⊥AB于E,设BE =a,?
∵∠ABP =180°-∠ABC =60°,?
∴∠BPE =30°.∴BP =2BE =2a.?
在Rt△BPE中,PE =![]() =
=![]() .?
.?
∵PA切⊙O于A,∴∠OAP =90°.?
∵∠OAB =45°,∴∠PAE =45°.?
在Rt△PAE中,AE =PE =![]() ,?
,?
又∵AE +EB =AB =![]() ,?
,?
∴![]() ,解得
,解得![]() .?
.?
∴PB =2a =![]() -
-![]() .
.


科目:高中数学 来源: 题型:
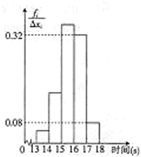 (2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
(2012•安徽模拟)为了了解某年级1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
(1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
 (2)根据k的取值范围,确定y=f(x)的定义域.
(2)根据k的取值范围,确定y=f(x)的定义域.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省揭阳市高三3月第一次高考模拟理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图1,在等腰梯形CDEF中,CB、DA是梯形的高,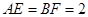 ,
,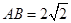 ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使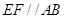 且
且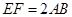 ,得一简单组合体
,得一简单组合体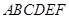 如图2示,已知
如图2示,已知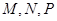 分别为
分别为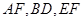 的中点.
的中点.
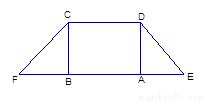
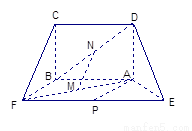
图1 图2
(1)求证: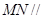 平面
平面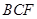 ;
;
(2)求证: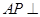
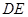 ;
;
(3)当 多长时,平面
多长时,平面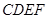 与平面
与平面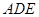 所成的锐二面角为
所成的锐二面角为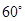 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
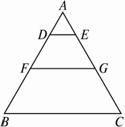
图1-3-14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com