
【题目】已知函数![]() ,
,![]() 。
。
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性。
的单调性。
【答案】(Ⅰ)a=3;(Ⅱ)答案见解析.
【解析】
(Ⅰ)先求出f(x)的导数f′(x),再根据![]() ,即可求得
,即可求得![]() 的值;
的值;
(Ⅱ)由题意可知,f(x)的定义域为(0,+∞),![]() ,令f′(x)=0,得x1=1,x2=a1.据此分类讨论函数的单调性即可.
,令f′(x)=0,得x1=1,x2=a1.据此分类讨论函数的单调性即可.
(Ⅰ)由题意可得:![]() ,故
,故![]() ,∴
,∴![]() .
.
(Ⅱ)∵函数![]() ,其中a>1,
,其中a>1,
∴f(x)的定义域为(0,+∞),![]() ,
,
令f′(x)=0,得x1=1,x2=a1.
①若a1=1,即a=2时,![]() ,故f(x)在(0,+∞)单调递增.
,故f(x)在(0,+∞)单调递增.
②若0<a1<1,即1<a<2时,
由f′(x)<0得,a1<x<1;
由f′(x)>0得,0<x<a1,或x>1.
故f(x)在(a1,1)单调递减,在(0,a1),(1,+∞)单调递增.
③若a1>1,即a>2时,
由f′(x)<0得,1<x<a1;由f′(x)>0得,0<x<1,或x>a1.
故f(x)在(1,a1)单调递减,在(0,1),(a1,+∞)单调递增.
综上可得,当a=2时,f(x)在(0,+∞)单调递增;
当1<a<2时,f(x)在(a1,1)单调递减,在(0,a1),(1,+∞)单调递增;
当a>2时,f(x)在(1,a1)单调递减,在(0,1),(a1,+∞)单调递增.


科目:高中数学 来源: 题型:
【题目】为了调查观众对电影“复仇者联盟4”结局的满意程度,研究人员在某电影院随机抽取了1000名观众作调查,所得结果如下所示,其中不喜欢“复仇者联盟4”的结局的观众占被调查观众总数的![]() .
.
男性观众 | 女性观众 | 总计 | |
喜欢“复仇者联盟4”的结局 | 400 | ||
不喜欢“复仇者联盟4”的结局 | 200 | ||
总计 |
(Ⅰ)完善上述![]() 列联表;
列联表;
(Ⅱ)是否有99.9%的把握认为观众对电影“复仇者联盟4”结局的满意程度与性别具有相关性?
附: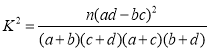
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
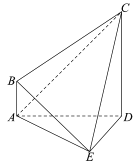
(1)求棱锥![]() 的体积;
的体积;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() 分别是
分别是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 折起,下列说法正确的是__________(填上所有正确的序号).
折起,下列说法正确的是__________(填上所有正确的序号).
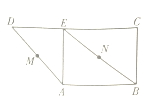
①不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内)都有
内)都有![]() 平面
平面![]() ;
;
②不论![]() 折至何位置都有
折至何位置都有![]() ;
;
③不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内)都有
内)都有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com