
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴正半轴上,点
轴正半轴上,点![]() 到其准线的距离等于
到其准线的距离等于![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
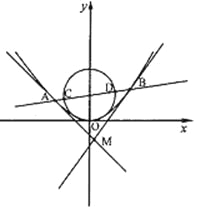
(Ⅱ)如图,过抛物线![]() 的焦点的直线从左到右依次与抛物线
的焦点的直线从左到右依次与抛物线![]() 及圆
及圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,试证明
四点,试证明![]() 为定值.
为定值.
(Ⅲ)过![]() 、
、![]() 分别作抛物
分别作抛物![]() 的切线
的切线![]() 、
、![]() ,且
,且![]() 、
、![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 面积之和的最小值.
面积之和的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)设抛物线![]() 的方程为
的方程为![]() ,根据已知条件得出
,根据已知条件得出![]() 的值,可得出抛物线
的值,可得出抛物线![]() 的方程;
的方程;
(Ⅱ)解法一:求出抛物线![]() 的焦点
的焦点![]() 的坐标,设直线
的坐标,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,并列出韦达定理,利用抛物线的定义并结合韦达定理证明出
的方程联立,并列出韦达定理,利用抛物线的定义并结合韦达定理证明出![]() 是定值;
是定值;
解法二:设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,并列出韦达定理,并利用弦长公式并结合韦达定理证明
的方程联立,并列出韦达定理,并利用弦长公式并结合韦达定理证明![]() 是定值;
是定值;
(Ⅲ)利用导数求出切线![]() 、
、![]() 的方程,并将两切线方程联立得出交点
的方程,并将两切线方程联立得出交点![]() 的坐标,并计算出点
的坐标,并计算出点![]() 到直线
到直线![]() 的距离
的距离![]() ,可计算出
,可计算出![]() 和
和![]() 的面积和,换元
的面积和,换元![]() ,利用导数法求出
,利用导数法求出![]() 和
和![]() 的面积和的最小值.
的面积和的最小值.
(Ⅰ)设抛物线方程为![]() ,由题意得
,由题意得![]() ,得
,得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() ;
;
(Ⅱ) 解法一:抛物线![]() 的焦点与
的焦点与![]() 的圆心重合,即为
的圆心重合,即为![]() .
.
设过抛物线焦点的直线方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立
的方程联立![]() ,消去
,消去![]() 并整理得
并整理得![]() ,
,
![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() .
.
由抛物线的定义可知![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,即
,即![]() 为定值
为定值![]() ;
;
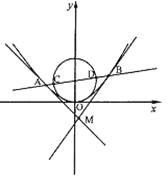
解法二:设过抛物线焦点的直线方程为![]() ,设点
,设点![]() 、
、![]() ,
,
不妨设![]() ,
,![]() .
.
将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立
的方程联立![]() ,消去
,消去![]() 并整理得
并整理得![]() ,
,
![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]()
![]() ,
,
即![]() 为定值
为定值![]() ;
;
(Ⅲ)![]() ,
,![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
同理可得,切线![]() 的方程为
的方程为![]() ,
,
联立两切线方程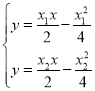 ,解得
,解得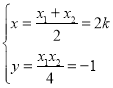 ,即点
,即点![]() ,
,
所以点![]() 到直线
到直线![]() 的距离为
的距离为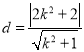 .
.
设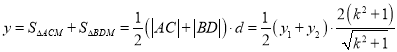
![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,即当
时,即当![]() 时,
时,![]() ,即
,即![]() 和
和![]() 面积之和的最小值为
面积之和的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
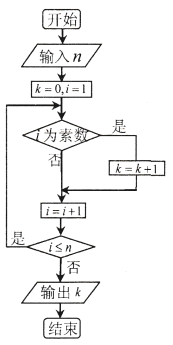
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新冠肺炎疫情的影响下,南充高中响应“停课不停教,停课不停学”的号召进行线上教学,高二年级的甲乙两个班中,需根据某次数学测试成绩选出某班的5名学生参加数学竞赛决赛,已知这次测试他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.

(1)求出x,y的值,且分别求甲乙两个班中5名学生成绩的方差![]() ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: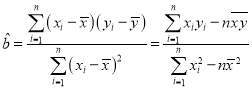 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2-x+16a)的定义域为R;命题q:不等式3x-9x<a对任意x∈R恒成立.
(1)如果p是真命题,求实数a的取值范围;
(2)如果命题“p或q”为真命题且“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 左、右顶点分别为A、B,上顶点为D(0,1),离心率为
左、右顶点分别为A、B,上顶点为D(0,1),离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)若点E是椭圆C上位于x轴上方的动点,直线AE、BE与直线![]() 分别交于M、N两点,当线段MN的长度最小时,椭圆C上是否存在点T使
分别交于M、N两点,当线段MN的长度最小时,椭圆C上是否存在点T使![]() 的面积为
的面积为![]() ?若存在,求出点T的坐标:若不存在,请说明理由.
?若存在,求出点T的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]() (
(![]() ),且
),且![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]() (
(![]() ),都存在
),都存在![]() ,使得
,使得![]() ,写出你的探究过程,并求出满足条件的正实数
,写出你的探究过程,并求出满足条件的正实数![]() 的集合.
的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z满足|z|![]() ,z的实部大于0,z2的虚部为2.
,z的实部大于0,z2的虚部为2.
(1)求复数z;
(2)设复数z,z2,z﹣z2之在复平面上对应的点分别为A,B,C,求(![]() )
)![]()
![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com