
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]() (
(![]() ),且
),且![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]() (
(![]() ),都存在
),都存在![]() ,使得
,使得![]() ,写出你的探究过程,并求出满足条件的正实数
,写出你的探究过程,并求出满足条件的正实数![]() 的集合.
的集合.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)根据等差数列![]() 由
由![]() ,
,![]() 解得
解得![]() , 则得a.
, 则得a.
(2)由![]() ,解得
,解得![]() , 由
, 由![]() ,且
,且![]() ,
,![]() ,求得
,求得![]() 为奇数时与
为奇数时与![]() 为偶数时的
为偶数时的![]() ,利用等差数列的定义证得
,利用等差数列的定义证得![]() 是等差数列.
是等差数列.
(3)由题意![]() , 根据对任意
, 根据对任意![]() ,都有
,都有![]() ,分别讨论当
,分别讨论当![]() 时和当
时和当![]() 时,通过找反例得到数列
时,通过找反例得到数列![]() 不具有性质
不具有性质![]()
又当![]() 时,通过
时,通过![]() ,且
,且![]() ,得到
,得到![]() ,证得数列
,证得数列![]() 具有性质
具有性质![]() .
.
(1)设等差数列![]() 的公差为
的公差为![]() .由
.由![]() ,
,![]() 得
得![]() ,
,
解得![]() . 则得
. 则得 ![]() ,所以a=3.
,所以a=3.
(2)由![]() ,得
,得 ![]() ,
,
解得![]() , 由
, 由![]() ,且
,且![]() ,
,![]() ,得
,得
当![]() 为奇数时,
为奇数时,![]() ;
;
当![]() 为偶数时,
为偶数时,![]() .
.
所以对任意![]() ,都有
,都有![]() ,当
,当![]() 时,
时,![]() ,
,
所以数列![]() 是以
是以![]() 为首项、
为首项、![]() 为公差的等差数列.
为公差的等差数列.
(3)由题意![]() ,
,
①当![]() 时,
时,![]() ,
,
所以对任意![]() ,都有
,都有![]() ,
,
因此数列![]() 不具有性质
不具有性质![]() .
.
②当![]() 时,
时,![]() ,
,![]() ,
,
所以对任意![]() ,都有
,都有![]() ,
,
因此数列![]() 不具有性质
不具有性质![]() .
.
③当1<a<2时,![]()
![]() ,
,
![]() ,
,
取![]() (
(![]() 表示不小于
表示不小于![]() 的最小整数),则
的最小整数),则![]() ,
,![]() .
.
所以对于任意![]() ,
,![]() ,
,
即对于任意![]() ,
,![]() 都不在区间
都不在区间![]() 内,
内,
所以数列![]() 不具有性质
不具有性质![]() .
.
④当![]() 时,
时,![]() ,且
,且![]() ,
,
即对任意的![]() ,都有
,都有![]() ,
,
所以当![]() 时,数列
时,数列![]() 具有性质
具有性质![]() .
.
综上,使得数列![]() 具有性质
具有性质![]() 的正实数
的正实数![]() 的集合为
的集合为![]() .
.
③④的另解:
当![]() 时,
时,![]() 单调递增,
单调递增,![]() 单调递增,且
单调递增,且![]() 时,
时,![]() .
.
若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,即存在
,即存在![]() 在区间
在区间![]() 内.
内.
观察![]() ,
,![]() ,…,
,…,
发现在![]() 内的
内的![]() 只能是
只能是![]() .
.
证明:在![]() 个区间
个区间![]() ,
,![]() ,…,
,…,![]() 内需要
内需要![]() 个
个![]() ,
,
因为![]() ,
,![]() ,所以可选择的
,所以可选择的![]() 只能是
只能是![]() ,共
,共![]() 个.
个.
由![]() ,得
,得![]() .
.
所以只需满足![]() 恒成立,即
恒成立,即![]() ,
,
得![]() 对任意
对任意![]() 都成立.
都成立.
因为数列![]() 单调递增,且
单调递增,且![]() ,所以
,所以![]() .
.
综上,使得数列![]() 具有性质
具有性质![]() 的正实数
的正实数![]() 的集合为
的集合为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图 ,在棱长为 a 的正方体ABCD-A1 B1C1 D1 中,E 、F 分别 是棱 AB 与BC 的中点.
(1)求二 面角 B-FB1-E 的大小;
(2)求点 D 到平面B1EF 的距离;
(3)在棱 DD1 上能否找到一点 M, 使 BM ⊥平面EFB1 ? 若能, 试确定点 M 的位置;若不能, 请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.
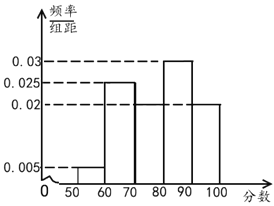
青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 为
为![]() 上异于顶点的任意一点,过
上异于顶点的任意一点,过![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,且有
,且有![]() ,当点
,当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和
和![]() 相切于点
相切于点![]() ,试问直线
,试问直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() ,点F、E分别是BC、CD的中点,现沿AE将
,点F、E分别是BC、CD的中点,现沿AE将![]() 折起,使点D至点M的位置,且
折起,使点D至点M的位置,且![]() .
.


(1)证明:![]() 平面MEF;
平面MEF;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com