
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
【答案】(1)3,2,1 (2)![]()
【解析】
(1)从小学、中学、大学中分别抽取的学校数目为3、2、1.
(2)①在抽取到的6所学校中,3所小学分别记为A1,A2,A3,2所中学分别记为A4,A5,大学记为A6,则抽取2所学校的所有可能结果为{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共15种.
②从6所学校中抽取的2所学校均为小学(记为事件B)的所有可能结果为{A1,A2},{A1,A3},{A2,A3},共3种.
所以P(B)=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为 ![]() 和
和 ![]() .现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
.现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】π为圆周率,e=2.71828…为自然对数的底数.
(1)求函数f(x)= ![]() 的单调区间;
的单调区间;
(2)求e3 , 3e , eπ , πe , 3π , π3这6个数中的最大数和最小数;
(3)将e3 , 3e , eπ , πe , 3π , π3这6个数按从小到大的顺序排列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知标准方程下的椭圆![]() 的焦点在
的焦点在![]() 轴上,且经过点
轴上,且经过点 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线![]() 的焦点重合.椭圆
的焦点重合.椭圆![]() 的上顶点为
的上顶点为![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,连接
两点,连接![]() 、
、![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
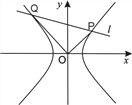
【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C: ![]() +
+ ![]() =1,直线l:
=1,直线l: ![]() (t为参数)
(t为参数)
(1)写出曲线C的参数方程,直线l的普通方程.
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
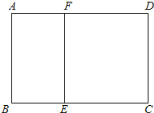
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com