Question

【题目】已知矩阵A的逆矩阵A﹣1=（ ）．
（1）求矩阵A；
（2）求矩阵A﹣1的特征值以及属于每个特征值的一个特征向量．

Answer 1

【答案】
（1）解：设A= ，则由AA﹣1=E得 = ，

解得a= ，b=﹣ ，c=﹣ ，d= ，所以A=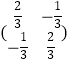

（2）解：矩阵A﹣1的特征多项式为f（λ）= =（λ﹣2）2﹣1，

令f（λ）=（λ﹣2）2﹣1=0，可求得特征值为λ1=1，λ2=3，

设λ1=1对应的一个特征向量为α= ，

则由λ1α=Mα，得x+y=0

得x=﹣y，可令x=1，则y=﹣1，

所以矩阵M的一个特征值λ1=1对应的一个特征向量为 ，

同理可得矩阵M的一个特征值λ2=3对应的一个特征向量为

【解析】（1）利用AA﹣1=E，建立方程组，即可求矩阵A；（2）先根据特征值的定义列出特征多项式，令f（λ）=0解方程可得特征值，再由特征值列出方程组即可解得相应的特征向量．