
【题目】π为圆周率,e=2.71828…为自然对数的底数.
(1)求函数f(x)= ![]() 的单调区间;
的单调区间;
(2)求e3 , 3e , eπ , πe , 3π , π3这6个数中的最大数和最小数;
(3)将e3 , 3e , eπ , πe , 3π , π3这6个数按从小到大的顺序排列,并证明你的结论.
【答案】
(1)解:函数f(x)的定义域为(0,+∞),
∵f(x)= ![]() ,∴f′(x)=
,∴f′(x)= ![]() ,
,
当f′(x)>0,即0<x<e时,函数f(x)单调递增;
当f′(x)<0,即x>e时,函数f(x)单调递减.
故函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞).
(2)解:∵e<3<π,
∴eln3<elnπ,πlne<πln3,即ln3e<lnπe,lneπ<ln3π.
于是根据函数y=lnx,y=ex,y=πx在定义域上单调递增,可得3e<πe<π3,e3<eπ<3π,
故这六个数的最大数在π3与3π之中,最小数在3e与e3之中.
由e<3<π及(1)的结论,得f(π)<f(3)<f(e),即 ![]() ,
,
由 ![]() ,得lnπ3<ln3π,∴3π>π3;
,得lnπ3<ln3π,∴3π>π3;
由 ![]() ,得ln3e<lne3,∴3e<e3.
,得ln3e<lne3,∴3e<e3.
综上,6个数中的最大数是3π,最小数是3e.
(3)证明:由(2)知,3e<πe<π3<3π,3e<e3,
又由(2)知, ![]() ,得πe<eπ,
,得πe<eπ,
故只需比较e3与πe和eπ与π3的大小.
由(1)知,当0<x<e时,f(x)<f(e)= ![]() ,即
,即 ![]() .
.
在上式中,令x= ![]() ,又
,又 ![]() ,则ln
,则ln ![]() <
< ![]() ,
,
从而2﹣lnπ ![]() ,即得lnπ
,即得lnπ ![]() .①
.①
由①得,elnπ>e(2﹣ ![]() )>2.7×(2﹣
)>2.7×(2﹣ ![]() )>2.7×(2﹣0.88)=3.024>3,即elnπ>3,亦即lnπe>lne3,
)>2.7×(2﹣0.88)=3.024>3,即elnπ>3,亦即lnπe>lne3,
∴e3<πe.
又由①得,3lnπ>6﹣ ![]() >6﹣e>π,即3lnπ>π,
>6﹣e>π,即3lnπ>π,
∴eπ<π3.
综上可得,3e<e3<πe<eπ<π3<3π,即6个数从小到大顺序为3e,e3,πe,eπ,π3,3π.
【解析】(1)先求函数定义域,然后在定义域内解不等式f′(x)>0,f′(x)<0即可得到单调增、减区间;(2)由e<3<π,得eln3<elnπ,πlne<πln3,即ln3e<lnπe , lneπ<ln3π . 再根据函数y=lnx,y=ex , y=πx在定义域上单调递增,可得3e<πe<π3 , e3<eπ<3π , 从而六个数的最大数在π3与3π之中,最小数在3e与e3之中.由e<3<π及(1)的结论,得f(π)<f(3)<f(e),即 ![]() ,由此进而得到结论;(3)由(2)可知,3e<πe<π3<3π , 3e<e3 , 又由(2)知,
,由此进而得到结论;(3)由(2)可知,3e<πe<π3<3π , 3e<e3 , 又由(2)知, ![]() ,得πe<eπ , 故只需比较e3与πe和eπ与π3的大小.由(1)可得0<x<e时,
,得πe<eπ , 故只需比较e3与πe和eπ与π3的大小.由(1)可得0<x<e时, ![]() ,令x=
,令x= ![]() ,有ln
,有ln ![]() <
< ![]() ,从而2﹣lnπ
,从而2﹣lnπ ![]() ,即得lnπ
,即得lnπ ![]() .①,由①还可得lnπe>lne3 , 3lnπ>π,由此易得结论;
.①,由①还可得lnπe>lne3 , 3lnπ>π,由此易得结论;
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,且2a5-a3=13,S4=16.
(1)求数列{an}的前n项和Sn;
(2)设Tn=![]() (-1)iai,若对一切正整数n,不等式 λTn<[an+1+(-1)n+1an]·2n-1 恒成立,求实数 λ 的取值范围;
(-1)iai,若对一切正整数n,不等式 λTn<[an+1+(-1)n+1an]·2n-1 恒成立,求实数 λ 的取值范围;
(3)是否存在正整数m,n(n>m>2),使得S2,Sm-S2,Sn-Sm成等比数列?若存在,求出所有的m,n;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线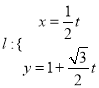 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
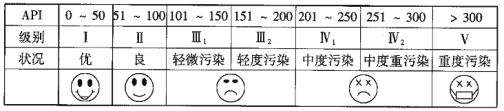
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到频率分布条形图如图.
进行分组,得到频率分布条形图如图.
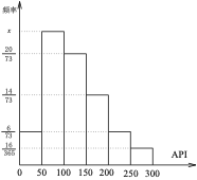
(1)求图中![]() 的值;
的值;
(2)空气质量状况分别为轻微污染或轻度污染定为空气质量Ⅲ级,求一年中空气质量为Ⅲ级的天数
(3)小张到该城市出差一天,这天空气质量为优良的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求:
①顾客所获的奖励额为60元的概率;
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com