
【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
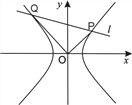
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
【答案】![]() 1
1![]()
![]() ;
;![]() 2
2![]() .
.
【解析】试题分析:
(Ⅰ) 由![]() ,可得
,可得![]() ,故双曲线方程为
,故双曲线方程为![]() ,代入点
,代入点![]() 的坐标可得
的坐标可得![]() ,由此可得双曲线方程. (Ⅱ)根据直线
,由此可得双曲线方程. (Ⅱ)根据直线![]() 的斜率存在与否分两种情况求解.当斜率存在时,可根据一元二次方程根与系数的关系及两点间的距离公式求解即可.当斜率不存在时直接计算可得结果.
的斜率存在与否分两种情况求解.当斜率存在时,可根据一元二次方程根与系数的关系及两点间的距离公式求解即可.当斜率不存在时直接计算可得结果.
试题解析:
(1)由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴ 双曲线方程为![]() ,
,
∵ 点![]() 在双曲线上,
在双曲线上,
∴![]() ,
,
解得 ![]() ,
,
∴ 双曲线的方程为![]() .
.
(2)①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直线![]() 与双曲线交于
与双曲线交于![]() 两点,
两点,
∴![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
由![]() 得到:
得到:![]() ,
,
即![]() ,
,
∴![]() ,
,
化简得![]() .
.
∴![]() ,
,
当![]() 时上式取等号,且方程(*)有解.
时上式取等号,且方程(*)有解.
②当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 的方程为
的方程为![]() ,则有
,则有![]() ,
,
由![]() 可得
可得![]() ,
,
可得![]() ,解得
,解得![]() .
.
∴![]() .
.
∴![]()
![]() .
.
综上可得![]() 的最小值是24.
的最小值是24.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,|an+1﹣an|=pn , n∈N* .
(1)若{an}是递增数列,且a1 , 2a2 , 3a3成等差数列,求p的值;
(2)若p= ![]() ,且{a2n﹣1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式.
,且{a2n﹣1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
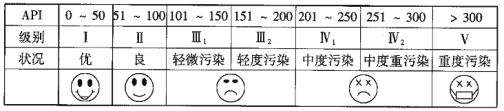
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,得到频率分布条形图如图.
进行分组,得到频率分布条形图如图.
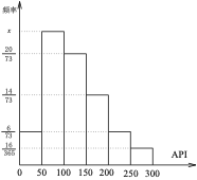
(1)求图中![]() 的值;
的值;
(2)空气质量状况分别为轻微污染或轻度污染定为空气质量Ⅲ级,求一年中空气质量为Ⅲ级的天数
(3)小张到该城市出差一天,这天空气质量为优良的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.已知函数
的不动点.已知函数![]()
![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求
恒有两个相异的不动点,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的两个不动点为
的两个不动点为![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com