【题目】已知
.
（1）若
的两根分别为某三角形两内角的正弦值，求m的取值范围；
（2）问是否存在实数m，使得的两根是直角三角形两个锐角的正弦值.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】在古装电视剧《知否》中，甲乙两人进行一种投壶比赛，比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种，其中“有初”算“两筹”，“贯耳”算“四筹”，“散射”算“五筹”，“双耳”算“六筹”，“依竿”算“十筹”，三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为
，投中“贯耳”的概率为
，投中“散射”的概率为
，投中“双耳”的概率为
，投中“依竿”的概率为
，乙的投掷水平与甲相同，且甲乙投掷相互独立.比赛第一场，两人平局;第二场，甲投了个“贯耳”，乙投了个“双耳”，则三场比赛结束时，甲获胜的概率为( )
A.
B.
C.D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知△
的三个内角
、
、
所对应的边分别为
、
、
，复数
，
，（其中
是虚数单位），且
.
（1）求证：
，并求边长的值；
（2）判断△的形状，并求当
时，角的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，且
，
.
（1）若数列是等差数列，且
，求实数
的值；
（2）若数列满足
（
），且
，求证：是等差数列；
（3）设数列是等比数列，试探究当正实数满足什么条件时，数列具有如下性质
：对于任意的
（），都存在
，使得
，写出你的探究过程，并求出满足条件的正实数的集合.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P－ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝
，PA＝AD＝2，AB＝BC＝1，点M、E分别是PA、PD的中点
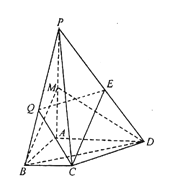
(1)求证：CE//平面BMD
(2)点Q为线段BP中点，求直线PA与平面CEQ所成角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
，在
处的切线方程为
.
（1）求
， 
；
（2）若
，证明： 
.
【答案】（1）
， 
；（2）见解析
【解析】试题分析：（1）求出函数的导数，得到关于
的方程组，解出即可；
（2）由（1）可知
， 
，
由
，可得
，令
， 利用导数研究其单调性可得
，
从而证明
.
试题解析：（（1）由题意
，所以
，
又
，所以
，
若
，则
，与
矛盾，故
， 
.
（2）由（1）可知
， 
，
由
，可得
，
令
，
，
令
当
时， 
， 
单调递减，且
；
当
时， 
， 
单调递增；且
，
所以
在
上当单调递减，在
上单调递增，且
，
故
，
故
.
【点睛】本题考查利用函数的切线求参数的方法，以及利用导数证明不等式的方法，解题时要认真审题，注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
， 
为参数），以坐标原点
为极点， 
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
，若直线
与曲线
相切；
（1）求曲线
的极坐标方程；
（2）在曲线
上取两点
， 
与原点
构成
，且满足
，求面积
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列四个命题：
①函数
与函数
表示同一个函数；
②奇函数的图象一定通过直角坐标系的原点；
③函数
的图象可由
的图象向右平移1个单位得到；
④若函数
的定义域为
，则函数
的定义域为
；
⑤设函数是在区间
上图象连续的函数，且
，则方程
在区间上至少有一实根．
其中正确命题的序号是________．（填上所有正确命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题正确的是（ ）
A.已知随机变量
，若
.则
B.已知分类变量
与
的随机变量
的观察值为
，则当的值越大时，“与有关”的可信度越小.
C.在线性回归模型中，计算其相关指数
，则可以理解为：解析变量对预报变量的贡献率约为
D.若对于变量
与
的
组统计数据的线性回归模型中，相关指数
.又知残差平方和为
.那么
.（注意：
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
