【题目】如图，矩形ABCD中，
，
，点F、E分别是BC、CD的中点，现沿AE将
折起，使点D至点M的位置，且
.
（1）证明：
平面MEF；
（2）求二面角
的大小.
科目：高中数学 来源： 题型：
【题目】2019年12月以来，湖北省武汉市持续开展流感及相关疾病监测，发现多起病毒性肺炎病例，均诊断为病毒性肺炎/肺部感染，后被命名为新型冠状病毒肺炎（CoronaVirusDisease2019，COVID—19），简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
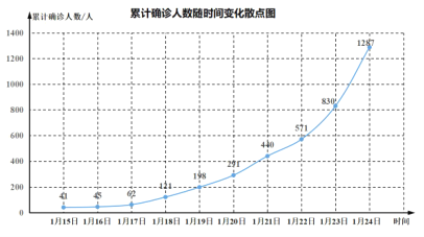
为了预测在未釆取强力措施下，后期的累计确诊人数，建立了累计确诊人数y与时间变量t的两个回归模型，根据1月15日至1月24日的数据（时间变量t的值依次1，2，…，10）建立模型
和
.
（1）根据散点图判断，与哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型？（给出判断即可，不必说明理由）
（2根据（1）的判断结果及附表中数据，建立y关于x的回归方程；
（3）以下是1月25日至1月29日累计确诊人数的真实数据，根据（2）的结果回答下列问题：
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
（ⅰ）当1月25日至1月27日这3天的误差（模型预测数据与真实数据差值的绝对值与真实数据的比值）都小于0.1则认为模型可靠，请判断（2）的回归方程是否可靠？
（ⅱ）2020年1月24日在人民政府的强力领导下，全国人民共同采取了强力的预防“新冠肺炎”的措施，若采取措施5天后，真实数据明显低于预测数据，则认为防护措施有效，请判断预防措施是否有效？
附：对于一组数据（
，
，……，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
.
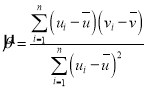参考数据：其中
，
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中，将底面为长方形且有一条侧棱与地面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑，首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马，如图所示，在阳马
中，
底面
.
（1）已知
，斜梁
与底面所成角为
，求立柱
的长；（精确到
）
（2）求证：四面体
为鳖臑.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，且
，
.
（1）若数列是等差数列，且
，求实数
的值；
（2）若数列满足
（
），且
，求证：是等差数列；
（3）设数列是等比数列，试探究当正实数满足什么条件时，数列具有如下性质
：对于任意的
（），都存在
，使得
，写出你的探究过程，并求出满足条件的正实数的集合.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在30人或30人以下,每人需交费用为900元；若旅行团人数多于30人,则给予优惠：每多1人,人均费用减少10元,直到达到规定人数75人为止．旅行社需支付各种费用共计15000元．
（1）写出每人需交费用
关于人数
的函数；
（2）旅行团人数为多少时,旅行社可获得最大利润？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
，在
处的切线方程为
.
（1）求
， 
；
（2）若
，证明： 
.
【答案】（1）
， 
；（2）见解析
【解析】试题分析：（1）求出函数的导数，得到关于
的方程组，解出即可；
（2）由（1）可知
， 
，
由
，可得
，令
， 利用导数研究其单调性可得
，
从而证明
.
试题解析：（（1）由题意
，所以
，
又
，所以
，
若
，则
，与
矛盾，故
， 
.
（2）由（1）可知
， 
，
由
，可得
，
令
，
，
令
当
时， 
， 
单调递减，且
；
当
时， 
， 
单调递增；且
，
所以
在
上当单调递减，在
上单调递增，且
，
故
，
故
.
【点睛】本题考查利用函数的切线求参数的方法，以及利用导数证明不等式的方法，解题时要认真审题，注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
， 
为参数），以坐标原点
为极点， 
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
，若直线
与曲线
相切；
（1）求曲线
的极坐标方程；
（2）在曲线
上取两点
， 
与原点
构成
，且满足
，求面积
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现某路口对一周内过往人员进行健康码检查安排7名工作人员进行值班，每人值班1天，每天1人，其中甲乙两人需要安排在相邻两天，且甲不排在周三，则不同的安排方法有( )
A.1440种B.1400种C.1320种D.1200种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年来，国资委.党委高度重视扶贫开发工作，坚决贯彻落实中央扶贫工作重大决策部署，在各个贫困县全力推进定点扶贫各项工作，取得了积极成效，某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积以及相应的管理时间的关系如下表所示：
土地使用面积 |
|
|
|
|
|
管理时间 |
|
|
|
|
|
并调查了某村
名村民参与管理的意愿，得到的部分数据如下表所示：
愿意参与管理 | 不愿意参与管理 | |
男性村民 |
|
|
女性村民 |
|
求出相关系数
的大小，并判断管理时间
与土地使用面积
是否线性相关？
若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况，则从该贫困县中任取
人，记取到不愿意参与管理的男性村民的人数为
，求的分布列及数学期望.
参考公式：
，参考数据：
，
，
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
