
【题目】如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 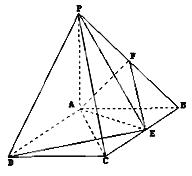
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在边BC的何处,都有PE⊥AF.
【答案】(1)见解析;(2)见解析。
【解析】试题分析:;(1)利用三角形的中位线及线面平行的判定定理解决;
(2)∵PA⊥平面ABCD,∴EB⊥PA又EB⊥AB,∴EB⊥平面PAB,又AF平面PAB,
∴AF⊥BE.又PA=AB=1,点F是PB的中点,∴AF⊥PB,所以可证出AF⊥平面PBE 则AF⊥PE易证得.
试题解析:
(1)当点E为BC的中点时,EF与平面PAC平行.
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC,又EF平面PAC,而PC平面PAC,
∴EF∥平面PAC.
(2)证明:
∵PA⊥平面ABCD,BE平面ABCD,
∴EB⊥PA,又EB⊥AB,AB∩AP=A,AB,AP平面PAB,
∴EB⊥平面PAB,又AF平面PAB,
∴AF⊥BE.
又PA=AB=1,点F是PB的中点,
∴AF⊥PB,
又∵PB∩BE=B,PB,BE平面PBE,
∴AF⊥平面PBE.
∵PE平面PBE,
∴AF⊥PE.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表,若成绩120分以上(含120分)为优秀.
分数区间 | 甲班频率 | 乙班频率 |
[0,30) | 0.1 | 0.2 |
[30,60) | 0.2 | 0.2 |
[60,90) | 0.3 | 0.3 |
[90,120) | 0.2 | 0.2 |
[120,150] | 0.2 | 0.1 |
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
(Ⅰ)求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成上面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧棱A1A⊥底面ABC,AC=1,AA1=2,∠BAC=90°,若直线AB1与直线A1C的夹角的余弦值是 ![]() ,则棱AB的长度是 .
,则棱AB的长度是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点. (Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形, ![]() ,求二面角C﹣AF﹣D大小.
,求二面角C﹣AF﹣D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() (如图2).
(如图2).

(1)证明:平面![]() 平面
平面![]() ;
;
(2)试在棱![]() 上确定一点
上确定一点![]() ,使截面
,使截面![]() 把几何体分成的两部分
把几何体分成的两部分![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com