
【题目】如图所示,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当几何体![]() 的体积等于
的体积等于![]() 时,求四棱锥
时,求四棱锥![]() 的侧面积.
的侧面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
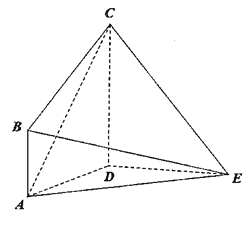
(1)连结BD,取CD的中点F,连结BF,证明BC⊥BD,BC⊥DE,即可证明BC⊥平面
BDE,推出BC⊥BE.(2)利用体积求出DE=2,然后求解EA,通过就是BE2=AB2+AE2,
证明AB⊥AE,然后求解四棱锥E﹣ABCD的侧面积.
(1)连结BD,取CD的中点F,连结BF,则直角梯形ABCD中,BF⊥CD,BF=CF=DF,
∴∠CBD=90°即:BC⊥BD
∵DE⊥平面ABCD,BC平面ABCD∴BC⊥DE
又BD∩DE=D∴BC⊥平面BDE
由BE平面BDE得:BC⊥BE
(2)∵![]() ,
,
∴DE=2
∴![]() ,
,![]() ,
,
又AB=2,∴BE2=AB2+AE2
∴AB⊥AE
∴四棱锥E﹣ABCD的侧面积为
![]()
![]()


科目:高中数学 来源: 题型:
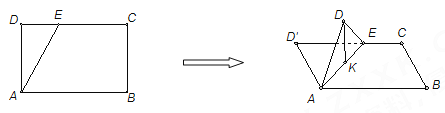
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一动点,现将
上一动点,现将![]() 沿
沿![]() 折起,使点
折起,使点![]() 在面
在面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,当点
上,当点![]() 从
从![]() 运动到
运动到![]() ,则点
,则点![]() 所形成轨迹的长度为( )
所形成轨迹的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行如图所示的程序框图,若输入a,b,c分别为1,2,0.3,则输出的结果为( ) 
A.1.125
B.1.25
C.1.3125
D.1.375
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若 ![]() (n∈N*),则称{an}是“紧密数列”;
(n∈N*),则称{an}是“紧密数列”;
(1)若a1=1, ![]() ,a3=x,a4=4,求x的取值范围;
,a3=x,a4=4,求x的取值范围;
(2)若{an}为等差数列,首项a1 , 公差d,且0<d≤a1 , 判断{an}是否为“紧密数列”;
(3)设数列{an}是公比为q的等比数列,若数列{an}与{Sn}都是“紧密数列”,求q的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),则y1 , y2 , …y2017的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣DEF中,侧面ABED是边长为2的菱形,且∠ABE= ![]() ,BC=
,BC= ![]() ,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=
,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM= ![]() CF.
CF.
(Ⅰ)证明:直线GM∥平面DEF;
(Ⅱ)求二面角M﹣AB﹣F的余弦值.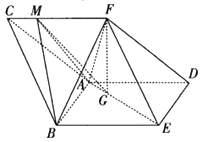
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,若椭圆与圆
,若椭圆与圆![]() :
:![]() 相交于M,N两点,且圆E在椭圆内的弧长为
相交于M,N两点,且圆E在椭圆内的弧长为![]() .
.
(1)求椭圆的方程;
(2)过椭圆的上焦点作两条相互垂直的直线,分别交椭圆于A,B、C,D,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足 ![]() ,则使不等式a2016>2017成立的所有正整数a1的集合为( )
,则使不等式a2016>2017成立的所有正整数a1的集合为( )
A.{a1|a1≥2017,a1∈N+}
B.{a1|a1≥2016,a1∈N+}
C.{a1|a1≥2015,a1∈N+}
D.{a1|a1≥2014,a1∈N+}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com