
 有且仅有两个不动点0、2.
有且仅有两个不动点0、2.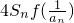 =1(Sn是数列{an}的前n项和),求证:
=1(Sn是数列{an}的前n项和),求证: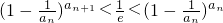 ;
;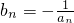 ,Tn是数列{bn}的前n项和,求证:T2012-1<ln2012<T2011.
,Tn是数列{bn}的前n项和,求证:T2012-1<ln2012<T2011. =x的不动点为0和2
=x的不动点为0和2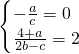 即
即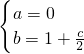 即b、c满足的关系式:b=1+
即b、c满足的关系式:b=1+ 且c≠0
且c≠0 (x≠1),
(x≠1),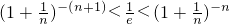 ,
, ,
, )<1<(n+1)ln(1+
)<1<(n+1)ln(1+ ),即证
),即证 <ln(1+
<ln(1+ )<
)< .
. <ln(x+1)<x(x>0)**.
<ln(x+1)<x(x>0)**. (x>0).
(x>0). ,h'(x)=
,h'(x)= ,
, <ln(x+1)<x.
<ln(x+1)<x. 则**式成立,∴
则**式成立,∴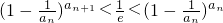 ,
, ,则Tn=
,则Tn=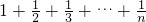
 <ln(1+
<ln(1+ )<
)< 中,令n=1,2,3,…,2011,并将各式相加,
中,令n=1,2,3,…,2011,并将各式相加,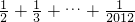 <ln
<ln +ln
+ln +…+ln
+…+ln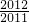 <1+
<1+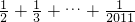 .
. =x的不动点为0和2,由此知
=x的不动点为0和2,由此知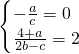 推出b、c满足的关系式.
推出b、c满足的关系式. (x≠1),2Sn=an-an2,且an≠1.所以an-an-1=-1,an=-n,要证待证不等式,只要证
(x≠1),2Sn=an-an2,且an≠1.所以an-an-1=-1,an=-n,要证待证不等式,只要证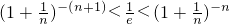 ,利用分析法证明
,利用分析法证明 <ln(1+
<ln(1+ )<
)< .考虑证不等式
.考虑证不等式 <ln(x+1)<x(x>0),由此入手利用函数的导数判断函数的单调性,然后导出
<ln(x+1)<x(x>0),由此入手利用函数的导数判断函数的单调性,然后导出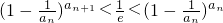 .
.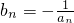 ,利用(2)的结论,通过累加法证明所要证明的不等式T2012-1<ln2012<T2011即可.
,利用(2)的结论,通过累加法证明所要证明的不等式T2012-1<ln2012<T2011即可.

科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+a |
| bx-c |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| e |
| 1 |
| an |
| 1 |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com